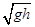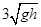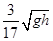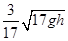题目内容
如图所示,一细木棍AB斜靠在地面与竖直墙壁之间。木棍AB与水平面之间的夹角为45°。A点到地面的距离为1m。已知重力加速度为10m/s2。空气阻力不计,现一跳蚤从竖直墙上距地面0.8m的C点以水平速度v0跳出,要到达细木棍上,水平速度v0至少为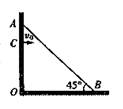
| A.1m/s | B.2m/s | C.2.5m/s | D.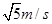 |
B
解析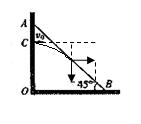
试题分析:据题意,据平抛运动规律可得当跳蚤跳到AB棍上时速度偏向角的正切值为:tan45°=vy /vx=gt/v0,速度偏向角的正切值是位移偏向角正切值的2倍,设位移偏向角为θ,则有tan45°=2tanθ,tanθ=1/2,由于棍与水平面夹角为45°,所以跳蚤从C点到AB棍的水平距离为0.8m,则跳蚤做平抛运动的水平距离为1.6m,而竖直距离为y=0.8m,所以跳蚤做平抛运动的时间为t,即:y=gt2/2,t=0.2s,则可以计算的跳蚤的水平速度为v0=gt=2m/s,所以B选项正确。
考点:本题考查对平抛运动的理解和应用。

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案物体在平抛运动的过程中,在相等的时间内,下列物理量相等的是( )
| A.速度的增量 | B.加速度 | C.位移 | D.平均速度 |
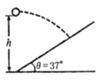
如图所示,小球以v0正对倾角为θ的斜面水平抛出,若小球到达斜面的位移最小,则飞行时间t为(重力加速度为g)( ) 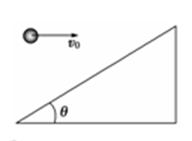
| A.v0tanθ | B.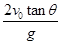 | C.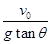 | D.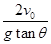 |
如图所示,在竖直面内有一个圆轨道,圆心为O。P为轨道上与O等高的最右端位置,一小球以某一初速度从p点水平向左抛出,落在圆轨道上的某一点,忽略一切阻力和能量损耗,则下列说法正确的是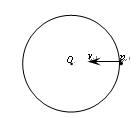
| A.小球初速度合适,可能垂直撞在圆轨道上 |
| B.小球初速度合适,位移大小等于直径 |
| C.初速度越大,落到圆轨道上的时间越长 |
| D.小球初速度合适,落在O点正下方的圆周上时间最长 |
如图所示是倾角为45°的斜坡,在斜坡底端P点正上方某一位置Q处以速度v0水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为t1.小球B从同一点Q处自由下落,下落至P点的时间为t2.不计空气阻力,则t1∶t2
| A.1∶2 | B.1∶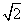 | C.1∶3 | D.1∶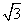 |
一位同学做飞镖游戏,已知圆盘直径为d,飞镖距圆盘为L,且对准圆盘上边缘的A点水平抛出,初速度为v0,飞镖抛出的同时,圆盘以垂直圆盘且过盘心O的水平轴匀速转动,角速度为w。若飞镖恰好击中A点,则下列关系中正确的是: ( )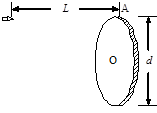
A.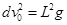 |
B. (n=0,1,2,¼) (n=0,1,2,¼) |
C.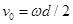 |
D.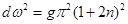 (n=0,1,2,¼) (n=0,1,2,¼) |
甲、乙两球位于同一竖直直线上的不同位置,甲比乙高出h。分别将甲、乙两球以v1、v2的速度沿同一水平方向抛出,不计空气阻力,下列条件中有可能使乙球击中甲球的是( )
A.同时抛出,且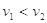 |
B.甲迟抛出,且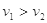 |
C.甲早抛出,且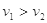 |
D.甲早抛出,且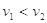 |