题目内容
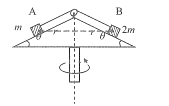
【题目】如图，在倾角为
的角锥体表面上对称地放着可视为质点的A、B两个物体，用一轻质绳跨过固定在顶部的光滑的定滑轮连接在一起，开始时绳子绷直但无张力。已知A、B两个物体的质量分别为m和2m，它们与竖直轴的距离均为r=1m，两物体与角锥体表面的动摩擦因数为0.8，认为最大静摩擦力等于滑动摩擦力，重力加速度为g=10m/s2，某时刻起，圆锥体绕竖直轴缓慢加速转动，加速转动过程中A、B两物体始终与角锥体保持相对静止，则下列说法正确的是（ ）
A.绳子没有张力之前，B物体受到的静摩擦力在增加
B.绳子即将有张力时，转动的角速度
C.在A、B滑动前A所受的静摩擦力一直在增加
D.在A、B即将滑动时，转动的角速度
【答案】AB
【解析】
A．绳子没有张力之前，对B物体进行受力分析后正交分解，根据牛顿第二定律可得
水平方向
竖直方向有
由以上两式可得，随着
的增大，f增大，N减小，选项A正确；
B．对B物体分析其将要发生滑动瞬间的临界状态时的受力可得
水平方向有
竖直方向有
代入数据解得
选项B正确；
C．在逐渐增大的过程中，A物体先有向外滑动的趋势，后有向内滑动的趋势，其所受静摩擦力先沿斜面向上增大，后沿斜面向上减小，再改为沿斜面向下增大，选项C错误；
D．增大到AB整体将要滑动时，B有向下滑动趋势，A有向上滑动趋势，对A物体
水平方向有
竖直方向有
对B物体
水平方向有
竖直方向有
联立以上四式解得
选项D错误。
故选AB。
练习册系列答案
相关题目
