题目内容
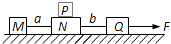 如图所示,三个质量不等的木块M、N、Q间用两根水平细线a、b相连,放在光滑水平面上.用水平向右的恒力F向右拉Q,使它们共同向右运动.这时细线a、b上的拉力大小分别为Ta、Tb.若在第2个木块N上再放一个小木块P,仍用水平向右的恒力F拉Q,使四个木块共同向右运动(P、N间无相对滑动),这时细线a、b上的拉力大小分别为Ta′、Tb′.下列说法中正确的是( )
如图所示,三个质量不等的木块M、N、Q间用两根水平细线a、b相连,放在光滑水平面上.用水平向右的恒力F向右拉Q,使它们共同向右运动.这时细线a、b上的拉力大小分别为Ta、Tb.若在第2个木块N上再放一个小木块P,仍用水平向右的恒力F拉Q,使四个木块共同向右运动(P、N间无相对滑动),这时细线a、b上的拉力大小分别为Ta′、Tb′.下列说法中正确的是( )分析:先对整体受力分析,受重力、支持力、拉力,根据牛顿第二定律列式求解加速度;然后再对M受力分析,受重力、支持力、拉力,再根据牛顿第二定律列式求解Ta;最后再对Q受力分析,受重力、支持力、拉力F和b绳子的拉力,根据牛顿第二定律列式求解Tb;在第2个木块N上再放一个小木块P,相当于N木块的重力变大,分析前面的表达式即可.
解答:解:先对整体受力分析,受重力、支持力、拉力,根据牛顿第二定律,有:F=(mM+mN+mQ)a ①
再对M受力分析,受重力、支持力、拉力,根据牛顿第二定律,有:Ta=mMa ②
对Q受力分析,受重力、支持力、拉力F和b绳子的拉力,根据牛顿第二定律,有:F-Tb=mQa ③
联立①②③解得:Ta=
;
Tb=
;
当在第2个木块N上再放一个小木块P,相当于N木块的重力变大,故Ta减小,Tb增加;
故选B.
再对M受力分析,受重力、支持力、拉力,根据牛顿第二定律,有:Ta=mMa ②
对Q受力分析,受重力、支持力、拉力F和b绳子的拉力,根据牛顿第二定律,有:F-Tb=mQa ③
联立①②③解得:Ta=
| mMF |
| mM+mN+mQ |
Tb=
| (mM+mN)F |
| mM+mN+mQ |
当在第2个木块N上再放一个小木块P,相当于N木块的重力变大,故Ta减小,Tb增加;
故选B.
点评:本题要灵活地选择研究对象,根据整体法求解加速度,根据隔离法求解系统内力,求解出表达式讨论是关键.

练习册系列答案
相关题目
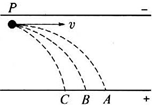 如图所示,三个质量相等的,分别带正电、负电和不带电的小球,以相同速率在竖直放置的带电平行金属板的P点沿垂直于电场方向水平射入电场,落在A、B、C三点,则( )
如图所示,三个质量相等的,分别带正电、负电和不带电的小球,以相同速率在竖直放置的带电平行金属板的P点沿垂直于电场方向水平射入电场,落在A、B、C三点,则( )| A、落到A点的小球带正电、落到B点的小球带负电、落到C点的小球不带电 | B、三小球在电场中运动时间相等 | C、三小球到达正极板的动能关系是EKA<EKb<EkC | D、三小球在电场中的加速度关系是aC>aB>aA |
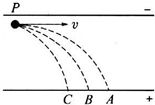 如图所示,三个质量相等的,分别带正电、负电和不带电的小球,以相同速率在竖直放置的带电平行金属板的P点沿垂直于电场方向水平射入电场,落在A、B、C三点,(要考虑重力)则( )
如图所示,三个质量相等的,分别带正电、负电和不带电的小球,以相同速率在竖直放置的带电平行金属板的P点沿垂直于电场方向水平射入电场,落在A、B、C三点,(要考虑重力)则( )| A、落到A点的小球带正电、落到B点的小球带负电、落到C点的小球不带电 | B、三小球在电场中运动时间相等 | C、三小球在电场中运动时间不相等 | D、三小球在电场中的加速度关系是aC>aB>aA |
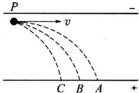 如图所示,三个质量相等的,分别带正电、负电和不带电的小球,以相同速率在带电平行金属板的P点沿垂直于电场方向射入电场,落在A、B、C三点,则.( )
如图所示,三个质量相等的,分别带正电、负电和不带电的小球,以相同速率在带电平行金属板的P点沿垂直于电场方向射入电场,落在A、B、C三点,则.( )| A、落到A点的小球带正电、落到B点的小球带负电、落到C点的小球不带电 | B、三小球在电场中运动时间相等 | C、三小球到达正极板的动能关系是EkA>EkB>EkC | D、三小球在电场中的加速度关系是aC>aB>aA |

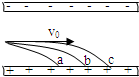 如图所示,三个质量相同且分别带有正电、负电和不带电的颗粒,从水平放置的平行带电金属板左侧以相同的速度v0沿垂直电场方向射入匀强电场,分别落在带正电荷的下极板上的a、b、c三点,则正电、负电和不带电这三个颗粒的下落点分别对应的是( )
如图所示,三个质量相同且分别带有正电、负电和不带电的颗粒,从水平放置的平行带电金属板左侧以相同的速度v0沿垂直电场方向射入匀强电场,分别落在带正电荷的下极板上的a、b、c三点,则正电、负电和不带电这三个颗粒的下落点分别对应的是( )