题目内容
1.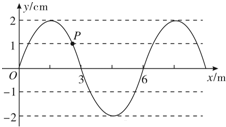 一列简谐横波沿x轴方向传播,在t=0时刻的波形如图所示,t=0.1s时,波形上P点的速度恰好第一次达到与t=0时刻的速度等值反向.若波沿x轴正方向传播,则波速v=20m/s;若波沿x轴负方向传播,则波速v=30m/s.
一列简谐横波沿x轴方向传播,在t=0时刻的波形如图所示,t=0.1s时,波形上P点的速度恰好第一次达到与t=0时刻的速度等值反向.若波沿x轴正方向传播,则波速v=20m/s;若波沿x轴负方向传播,则波速v=30m/s.
分析 利用质点带动法判断P点此刻的振动方向,根据质点P第一次达到与t=0时刻的速度等值反向的 时间与周期,读出波长,即可求得波速.
解答 解:(1)t=0时刻,x=0处的质点位于平衡位置,若波沿x轴正方向传播,则x=0处质点正在向下运动,
设该波的周期为T,则波动方程为:
$y=-Asinω(t-\frac{x}{v})=-A•sin\frac{2π}{T}(t-\frac{x}{v})$
由波的平移法可知,t=0时刻P点运动的方向向上,所以:${y}_{P}=-A•sin\frac{2π}{T}(t-\frac{{x}_{P}}{v})$,将P点纵坐标的位置代入可得:$\frac{{x}_{P}}{v}=\frac{5}{12}T$
又:λ=vT
所以:${x}_{P}=\frac{5}{12}T×v=\frac{5}{12}λ$=$\frac{5}{12}×6=2.5$m
同理可知,与P位移相等的点的平衡位置:$x′=\frac{1}{12}T×v=\frac{1}{12}λ=\frac{1}{12}×6=0.5$m
所以,若波沿x轴正方向传播,则经过0.1s的时间,x′处质点的振动传播到x=2.5m处的P点,高波传播的距离是:△x1=x-x′=2.5-0.5=2.0m
所以该波的传播速度:$v=\frac{△{x}_{1}}{t}=\frac{2.0}{0.1}=20$m/s
(2)t=0时刻,x=0处的质点位于平衡位置,若波沿x轴负方向传播,则x=0处质点正在向上运动,设该波的周期为T,则波动方程为:
$y=Asinω(t-\frac{x}{v})=A•sin\frac{2π}{T}(t-\frac{x}{v})$
由波的平移法可知,t=0时刻P点运动的方向向下,所以:${y}_{P}=A•sin\frac{2π}{T}(t-\frac{{x}_{P}}{v})$,
若t=0.1s时,波形上P点的速度恰好第一次达到与t=0时刻的速度等值反向,则由波形图可知,一定是x=4.5m--x=6m处某一点的振动传播到P点,将波动方程:
${y}_{x″}=A•sin\frac{2π}{T}(t-\frac{x″}{v})$
又:yx″=-0.01m
联立解得:$x″=\frac{11}{12}T•v=\frac{11}{12}λ=\frac{11}{12}×6$=5.5m
所以,若波沿x轴负方向传播,则经过0.1s的时间,x″处质点的振动传播到x=2.5m处的P点,高波传播的距离是:△x2=x″-x=5.5-2.5=3.0m
所以该波的传播速度:$v=\frac{△{x}_{1}}{t}=\frac{3.0}{0.1}=30$m/s
故答案为:20,30
点评 本题考查了波动方程和波传播的特点,能根据质点带动法判断质点振动方向.利用波形的平移法求解波传播的时间.

| A. | 经典力学是物理学和天文学的基础,也是现代工程技术的理论基础 | |
| B. | 经典力学的理论体系是经过几代科学家长期的探索,历经曲折才建立起来的 | |
| C. | 经典力学具有丰富的理论成果,也建立了验证科学的方法体系 | |
| D. | 当物体运动速度很大(v→c)、引力很强、活动空间很小(微观)时,经典力学理论所得的结果与实验结果之间出现了较大的偏差 |
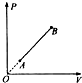
| A. | 气体从状态A变化到状态B,为等温变化 | |
| B. | 状态B时分子的平均动能大于状态A时的平均动能 | |
| C. | 由A到B过程中,气体对外做功 | |
| D. | 由A到B过程中,气体放出热量 |
| A. | 冬天,在结冰的公路上洒上沙子可以防滑 | |
| B. | 电磁灶可以加热砂锅里的食物 | |
| C. | 加油站工作人员穿化纤服装,是为了防止静电 | |
| D. | 一个额定功率200瓦的家用电冰箱,一天24小时的耗电量4.8千瓦时 |
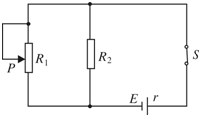 在图所示的电路中,电源电动势为E、内电阻为r.在滑动变阻器的滑动触头P从图示位置向下滑动的过程中( )
在图所示的电路中,电源电动势为E、内电阻为r.在滑动变阻器的滑动触头P从图示位置向下滑动的过程中( )| A. | 路端电压变大 | B. | 电路中的总电流变大 | ||
| C. | 通过电阻R2的电流变小 | D. | 通过滑动变阻器R1的电流变小 |
 如图所示,两物块A、B置于光滑水平面上,质量分别为m和2m,一轻质弹簧两端分别固定在两物块上,开始时弹簧处于拉伸状态,用手固定两物块.现在先释放物块B,当物块B的速度大小为3v时,再释放物块A,此时弹簧仍处于拉伸状态;当物块A的速度大小为v时,弹簧刚好恢复原长.自始至终弹簧都未超出弹性限度.求:
如图所示,两物块A、B置于光滑水平面上,质量分别为m和2m,一轻质弹簧两端分别固定在两物块上,开始时弹簧处于拉伸状态,用手固定两物块.现在先释放物块B,当物块B的速度大小为3v时,再释放物块A,此时弹簧仍处于拉伸状态;当物块A的速度大小为v时,弹簧刚好恢复原长.自始至终弹簧都未超出弹性限度.求:
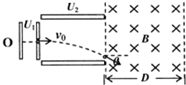 粒子扩束装置由粒子加速器,偏转电场和偏转磁场组成,如图,一个质量为m=2.0×10-11kg,电荷量q=1.0×10-5C的带正电微粒(重力忽略不计)从静止进入加速电场,电压U1=100V,加速后水平进入两平行金属板间的偏转电场中,金属板长L=20cm,两板间距d=10$\sqrt{3}$cm,微粒射出电场时速度偏转角θ=30°,接着进入一个方向垂直与纸面向里的匀强磁场,求:
粒子扩束装置由粒子加速器,偏转电场和偏转磁场组成,如图,一个质量为m=2.0×10-11kg,电荷量q=1.0×10-5C的带正电微粒(重力忽略不计)从静止进入加速电场,电压U1=100V,加速后水平进入两平行金属板间的偏转电场中,金属板长L=20cm,两板间距d=10$\sqrt{3}$cm,微粒射出电场时速度偏转角θ=30°,接着进入一个方向垂直与纸面向里的匀强磁场,求: 如图所示.MN是足够长的光滑绝缘水平轨道.质量为m的带正电A球,以水平速度υ0射向静止在轨道上带正电的B球,至A、B相距最近时,A球的速度变为$\frac{υ_0}{4}$,已知A、B两球始终没有接触.求:
如图所示.MN是足够长的光滑绝缘水平轨道.质量为m的带正电A球,以水平速度υ0射向静止在轨道上带正电的B球,至A、B相距最近时,A球的速度变为$\frac{υ_0}{4}$,已知A、B两球始终没有接触.求: