题目内容
14.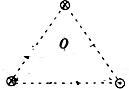 在一等边三角形的三个顶点上垂直纸面各放置一根长直通电导线,电流方向如图所示.设每根导线在中心O产生的磁感应强度大小为B0,则O点的磁感应强度大小为( )
在一等边三角形的三个顶点上垂直纸面各放置一根长直通电导线,电流方向如图所示.设每根导线在中心O产生的磁感应强度大小为B0,则O点的磁感应强度大小为( )| A. | 2B0 | B. | 3B0 | C. | $\sqrt{2}$B0 | D. | $\sqrt{3}$B0 |
分析 三角形中心O点到三根导线的距离相等.根据安培定则判断三根导线在O点产生的磁感应强度的方向,根据平行四边形定则进行合成,求出三根导线同时存在时的磁感应强度大小.
解答 解:根据安培定则判断得知:三根导线在O点产生的磁感应强度的方向分别为:
右边的导线产生的B方向左下方,大小为B0,与水平成60°角;
左边的导线产生的B方向右下方,大小为B0,与水平成60°角;
上面的导线产生的B方向水平向左,大小为B0;
则根据平行四边形定则进行合成可知,左边和上边的导线产生的合场强大小为B0,方向左下方,与水平成60°角,与右边的导线产生的磁场方向相同,
所以三根导线同时存在时的磁感应强度大小为2B0.
故选:A.
点评 本题首先运用安培定则判断B的方向,其次要利用平行四边形定则进行合成,同时要利用好几何关系.

练习册系列答案
相关题目
4.因“光纤之父”高锟的杰出贡献,中国科学院紫金山天文台1996年将一颗于1981年12月3日发现的国际编号为“3463”的小行星命名为“高锟星”.假设“高锟星”为均匀的球体,其质量为地球质量的$\frac{1}{k}$倍,半径为地球半径的$\frac{1}{q}$倍,则“高锟星”表面的重力加速度是地球表面的重力加速度的( )
| A. | $\frac{q}{k}$倍 | B. | $\frac{k}{q}$倍 | C. | $\frac{{q}^{2}}{k}$倍 | D. | $\frac{{k}^{2}}{q}$倍 |
2.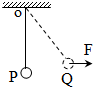 如图所示,一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平恒力F的作用下,从平衡位置P点移到Q点,轻绳偏离竖直方向的夹角为θ,在此过程中恒力F所做的功为( )
如图所示,一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平恒力F的作用下,从平衡位置P点移到Q点,轻绳偏离竖直方向的夹角为θ,在此过程中恒力F所做的功为( )
 如图所示,一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平恒力F的作用下,从平衡位置P点移到Q点,轻绳偏离竖直方向的夹角为θ,在此过程中恒力F所做的功为( )
如图所示,一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平恒力F的作用下,从平衡位置P点移到Q点,轻绳偏离竖直方向的夹角为θ,在此过程中恒力F所做的功为( )| A. | mgLcosθ | B. | FLsinθ | C. | mgL(1-cosθ) | D. | FLcosθ |
19. 在一个光滑水平面内建立直角坐标系xOy,质量为1kg的物体原来静止在坐标原点O(0,0),从t=0时刻受到如图所示随时间变化的外力作用,Fx表示沿x轴方向的外力,Fy表示沿y轴方向的外力,则( )
在一个光滑水平面内建立直角坐标系xOy,质量为1kg的物体原来静止在坐标原点O(0,0),从t=0时刻受到如图所示随时间变化的外力作用,Fx表示沿x轴方向的外力,Fy表示沿y轴方向的外力,则( )
 在一个光滑水平面内建立直角坐标系xOy,质量为1kg的物体原来静止在坐标原点O(0,0),从t=0时刻受到如图所示随时间变化的外力作用,Fx表示沿x轴方向的外力,Fy表示沿y轴方向的外力,则( )
在一个光滑水平面内建立直角坐标系xOy,质量为1kg的物体原来静止在坐标原点O(0,0),从t=0时刻受到如图所示随时间变化的外力作用,Fx表示沿x轴方向的外力,Fy表示沿y轴方向的外力,则( )| A. | 前2s内物体做匀加速曲线运动 | B. | 第3s末外力的功率为5W | ||
| C. | 4s末物体的坐标为(12m,8m) | D. | 第4s末物体的速度大小为8m/s |
6. 如图所示,轻质弹簧与中空的小球组成一个弹簧振子,振子在光滑水平杆上的a、b之间往复振动,O为它的平衡位置.若以向右为正方向,则( )
如图所示,轻质弹簧与中空的小球组成一个弹簧振子,振子在光滑水平杆上的a、b之间往复振动,O为它的平衡位置.若以向右为正方向,则( )
 如图所示,轻质弹簧与中空的小球组成一个弹簧振子,振子在光滑水平杆上的a、b之间往复振动,O为它的平衡位置.若以向右为正方向,则( )
如图所示,轻质弹簧与中空的小球组成一个弹簧振子,振子在光滑水平杆上的a、b之间往复振动,O为它的平衡位置.若以向右为正方向,则( )| A. | a、b两点处,振子的回复力相同 | |
| B. | 振子从b向O运动,动能逐渐减少 | |
| C. | 振子从a向O运动,加速度方向为正方向,加速度大小正在减少 | |
| D. | 振子从a向O运动经过c点时,位移方向为正方向,速度方向为正方向 |
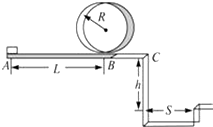 某校物理兴趣小组遥控赛车比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,比赛要求赛车顺利通过竖直圆轨道后继续在光滑平直轨道上运动到C点,并能越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=1.5w工作,进入竖直轨道前受到阻力恒为0.3N,随后在运动中受到的阻力均可不计.图中L=10.00m,R=0.32m,h=1.25m,S=1.50m.
某校物理兴趣小组遥控赛车比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,比赛要求赛车顺利通过竖直圆轨道后继续在光滑平直轨道上运动到C点,并能越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=1.5w工作,进入竖直轨道前受到阻力恒为0.3N,随后在运动中受到的阻力均可不计.图中L=10.00m,R=0.32m,h=1.25m,S=1.50m. 如图所示,ABC为一细圆管构成的$\frac{3}{4}$圆轨道,固定在竖直平面内,轨道半径为R(比细圆管的半径大得多),OA水平,OC竖直,最低点为B,最高点为C,细圆管内壁光滑.在A点正上方某位置处有一质量为m的小球(可视为质点)由静止开始下落,刚好进入细圆管内运动.已知细圆管的内径稍大于小球的直径,不计空气阻力.
如图所示,ABC为一细圆管构成的$\frac{3}{4}$圆轨道,固定在竖直平面内,轨道半径为R(比细圆管的半径大得多),OA水平,OC竖直,最低点为B,最高点为C,细圆管内壁光滑.在A点正上方某位置处有一质量为m的小球(可视为质点)由静止开始下落,刚好进入细圆管内运动.已知细圆管的内径稍大于小球的直径,不计空气阻力. 一束入射光从A点射入某圆柱形透明介质,经一次折射后到B点.已知该圆柱截面的半径为5cm,光线在A点的入射角α=45°,∠AOB=120°.求:
一束入射光从A点射入某圆柱形透明介质,经一次折射后到B点.已知该圆柱截面的半径为5cm,光线在A点的入射角α=45°,∠AOB=120°.求: