题目内容
5.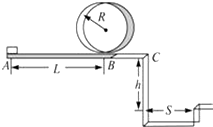 某校物理兴趣小组遥控赛车比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,比赛要求赛车顺利通过竖直圆轨道后继续在光滑平直轨道上运动到C点,并能越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=1.5w工作,进入竖直轨道前受到阻力恒为0.3N,随后在运动中受到的阻力均可不计.图中L=10.00m,R=0.32m,h=1.25m,S=1.50m.
某校物理兴趣小组遥控赛车比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,比赛要求赛车顺利通过竖直圆轨道后继续在光滑平直轨道上运动到C点,并能越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=1.5w工作,进入竖直轨道前受到阻力恒为0.3N,随后在运动中受到的阻力均可不计.图中L=10.00m,R=0.32m,h=1.25m,S=1.50m.问:(1)要使赛车顺利通过圆轨道,电动机至少工作多长时间?
(2)试分析说明赛车在恰能通过圆轨道的情况下能否顺利越过壕沟(取g=10m/s2 )
分析 (1)通过牛顿第二定律和动能定理求出小球要越过圆轨道最高点在B点的速度,通过平抛运动的轨道求出通过B点的速度,从而确定通过B点的最小速度,根据动能定理求出要使赛车完成比赛,电动机至少工作的时间.
(2)赛车在恰能通过圆轨道最高点时,由重力提供向心力,由牛顿第二定律求最高点的最小速度,再由机械能守恒求出赛车到达B点的速度,与上题中赛车刚好顺利越过壕沟时通过B点的速度比较,即可作出判断.
解答 解:(1)根据牛顿第二定律得,小球通过最高点的最小速度为v1,根据 mg=m$\frac{{v}_{1}^{2}}{R}$,得v1=$\sqrt{gR}$
根据动能定理得,mg•2R=$\frac{1}{2}m{v}_{B}^{2}$-$\frac{1}{2}m{v}_{1}^{2}$
解得赛车通过B点的最小速度 vB=$\sqrt{5gR}$=$\sqrt{5×10×0.32}$=4m/s.
故为保证过最高点,到达B点的速度至少为vB=4m/s
对于平抛运动过程,根据h=$\frac{1}{2}$gt′2得,t′=$\sqrt{\frac{2h}{g}}$=$\sqrt{\frac{2×1.25}{10}}$s=0.5s
则平抛运动初速度的最小值 v0=$\frac{s}{t}$=$\frac{1.5}{0.5}$=3m/s.
为保证越过壕沟,到达B点的速度至少为v0=3m/s
因此赛车到达B点的速度至少为:v=vB=4m/s
从A到B对赛车用动能定理:Pt-fL=$\frac{1}{2}m{v}^{2}$
解得t≥2.54s
(2)根据上题结果知,由于vB>v0,所以赛车在恰能通过圆轨道的情况下能顺利越过壕沟.
答:
(1)要使赛车完成比赛,电动机至少工作2.54s.
(2)赛车在恰能通过圆轨道的情况下能顺利越过壕沟.
点评 本题综合考查了动能定理、牛顿第二定律,涉及到直线运动、圆周运动、平抛运动,综合性较强,关键要把握圆周运动最高点的临界条件:重力提供向心力,运用运动的分解法研究平抛运动.

| A. | 行星的质量 | B. | 行星的半径 | C. | 恒星的质量 | D. | 恒星的半径 |
| A. | 0.2g | B. | 5g | C. | 2.5g | D. | 0.4g |
 如图所示,一个质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{3g}{4}$,这物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图所示,一个质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{3g}{4}$,这物体在斜面上上升的最大高度为h,则在这个过程中物体( )| A. | 重力势能增加了mgh | B. | 重力势能增加了$\frac{3mgh}{4}$ | ||
| C. | 动能损失了mgh | D. | 机械能损失了$\frac{mgh}{2}$ |
 如图所示,足够长的两条平行金属导轨竖直放置,其间有与导轨平面垂直的匀强磁场,两导轨通过导线与电流表A1、线圈M接在一起.N是绕在“□”形铁芯上的另一线圈,它与电流表A2组成闭合回路.现有一金属棒ab由静止释放,沿导轨下滑,下滑过程中与导轨接触良好,在ab下滑的过程中( )
如图所示,足够长的两条平行金属导轨竖直放置,其间有与导轨平面垂直的匀强磁场,两导轨通过导线与电流表A1、线圈M接在一起.N是绕在“□”形铁芯上的另一线圈,它与电流表A2组成闭合回路.现有一金属棒ab由静止释放,沿导轨下滑,下滑过程中与导轨接触良好,在ab下滑的过程中( )| A. | 通过电流表A1的电流是从左端流入的 | |
| B. | 通过电流表A2的电流是从左端流入的 | |
| C. | 电流表A1的示数逐渐增大 | |
| D. | 电流表A2的示数逐渐增大 |
| A. | 列车做匀加速直线运动 | B. | 列车做加速度逐渐减小的加速运动 | ||
| C. | 列车的速度先增大后减小 | D. | 列车的加速度先增大后减小 |
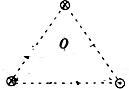 在一等边三角形的三个顶点上垂直纸面各放置一根长直通电导线,电流方向如图所示.设每根导线在中心O产生的磁感应强度大小为B0,则O点的磁感应强度大小为( )
在一等边三角形的三个顶点上垂直纸面各放置一根长直通电导线,电流方向如图所示.设每根导线在中心O产生的磁感应强度大小为B0,则O点的磁感应强度大小为( )| A. | 2B0 | B. | 3B0 | C. | $\sqrt{2}$B0 | D. | $\sqrt{3}$B0 |
 “天宫一号”(Tiangong-1)是中国第一个目标飞行器,于2011年9月29日21时16分3秒在酒泉卫星发射中心发射,2011年11月3日凌晨顺利实现与“神州八号”飞船的对接任务.某同学画出“天宫一号”和“神州八号”绕地球做匀速圆周运动的情境图,如图所示.图中A代表“天宫一号”,B代表“神州八号”,虚线为各自的轨道,由图可以判定( )
“天宫一号”(Tiangong-1)是中国第一个目标飞行器,于2011年9月29日21时16分3秒在酒泉卫星发射中心发射,2011年11月3日凌晨顺利实现与“神州八号”飞船的对接任务.某同学画出“天宫一号”和“神州八号”绕地球做匀速圆周运动的情境图,如图所示.图中A代表“天宫一号”,B代表“神州八号”,虚线为各自的轨道,由图可以判定( )| A. | “天宫一号”的运行速率一定大于7.9km/s | |
| B. | “天宫一号”的周期一定小于“神州八号”的周期 | |
| C. | “神州八号”需通过适度的加速才能与“天宫一号”实现对接 | |
| D. | “天宫一号”的向心加速度一定大于“神州八号”的向心加速度 |
 渔船常利用超声波来探测远处鱼群的方位.已知某超声波频率为1.0×105Hz,某时刻该超声波在水中传播的波动图象如图所示.
渔船常利用超声波来探测远处鱼群的方位.已知某超声波频率为1.0×105Hz,某时刻该超声波在水中传播的波动图象如图所示.