题目内容
6. 如图所示,轻质弹簧与中空的小球组成一个弹簧振子,振子在光滑水平杆上的a、b之间往复振动,O为它的平衡位置.若以向右为正方向,则( )
如图所示,轻质弹簧与中空的小球组成一个弹簧振子,振子在光滑水平杆上的a、b之间往复振动,O为它的平衡位置.若以向右为正方向,则( )| A. | a、b两点处,振子的回复力相同 | |
| B. | 振子从b向O运动,动能逐渐减少 | |
| C. | 振子从a向O运动,加速度方向为正方向,加速度大小正在减少 | |
| D. | 振子从a向O运动经过c点时,位移方向为正方向,速度方向为正方向 |
分析 振子做简谐振动,受到的回复力:F=-kx,振子的加速度:a=$\frac{F}{m}=-\frac{kx}{m}$;在振子做简谐振动的过程中,振子的动能与弹簧的弹性势能之间相互转化.
解答 解:A、振子做简谐振动,受到的回复力:F=-kx,可知a、b两点处,振子的回复力方向相反,是不相同的.故A错误;
B、振子从b向O运动的过程中,弹簧的弹性势能向振子的动能转化,动能逐渐增大.故B错误;
C、a在平衡位置O点的左侧,所以振子受到的回复力的方向向右;振子从a向O运动,回复力飞方向为正,加速度方向为正方向,加速度大小随位移的减小而正在减少.故C正确;
D、a和c点都在平衡位置O点的左侧,振子经过c点时,位移的方向为负.故D错误.
故选:C
点评 解决本题的关键要理解简谐运动的对称性,掌握其基本特征:F=-kx,能运用比例法研究加速度的关系.

练习册系列答案
相关题目
16.天文学家发现了某恒星有一颗行星在圆形轨道上绕其运动,并测出了行星的轨道半径和运行周期,已知引力常量G,由此可推算出( )
| A. | 行星的质量 | B. | 行星的半径 | C. | 恒星的质量 | D. | 恒星的半径 |
17.原来静止的列车在水平轨道上以恒定的功率启动,在启动后的一小段时间内(列车所受阻力恒定)( )
| A. | 列车做匀加速直线运动 | B. | 列车做加速度逐渐减小的加速运动 | ||
| C. | 列车的速度先增大后减小 | D. | 列车的加速度先增大后减小 |
14.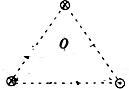 在一等边三角形的三个顶点上垂直纸面各放置一根长直通电导线,电流方向如图所示.设每根导线在中心O产生的磁感应强度大小为B0,则O点的磁感应强度大小为( )
在一等边三角形的三个顶点上垂直纸面各放置一根长直通电导线,电流方向如图所示.设每根导线在中心O产生的磁感应强度大小为B0,则O点的磁感应强度大小为( )
 在一等边三角形的三个顶点上垂直纸面各放置一根长直通电导线,电流方向如图所示.设每根导线在中心O产生的磁感应强度大小为B0,则O点的磁感应强度大小为( )
在一等边三角形的三个顶点上垂直纸面各放置一根长直通电导线,电流方向如图所示.设每根导线在中心O产生的磁感应强度大小为B0,则O点的磁感应强度大小为( )| A. | 2B0 | B. | 3B0 | C. | $\sqrt{2}$B0 | D. | $\sqrt{3}$B0 |
11.下列说法正确的是( )
| A. | 雷达是利用声波的反射来测定物体位置的设备 | |
| B. | 调谐是电磁波发射的过程,调制是电磁波接收的过程 | |
| C. | 微波是纵波,它是一种物质,其波长小于可见光的波长 | |
| D. | 在LC振荡电路中,电容器放电结束时,电路中的电流达到最大值 |
18.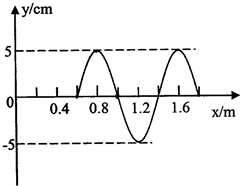 一列简谐横波在弹性介质中沿x轴传播,波源位于坐标原点O,零时刻时波源开始振动,t=0.6s时波源停止振动,如图为t=0.9s时的波形图.可以推知( )
一列简谐横波在弹性介质中沿x轴传播,波源位于坐标原点O,零时刻时波源开始振动,t=0.6s时波源停止振动,如图为t=0.9s时的波形图.可以推知( )
 一列简谐横波在弹性介质中沿x轴传播,波源位于坐标原点O,零时刻时波源开始振动,t=0.6s时波源停止振动,如图为t=0.9s时的波形图.可以推知( )
一列简谐横波在弹性介质中沿x轴传播,波源位于坐标原点O,零时刻时波源开始振动,t=0.6s时波源停止振动,如图为t=0.9s时的波形图.可以推知( )| A. | 波速为2m/s,周期为0.4s | |
| B. | 波源的起振方向沿y轴负方向 | |
| C. | 在t=1.2s时,x=1.0m处的质点位于波谷 | |
| D. | 从波源起振开始计时,2s内x=1.0m处的质点通过的总路程为100cm |
15. “天宫一号”(Tiangong-1)是中国第一个目标飞行器,于2011年9月29日21时16分3秒在酒泉卫星发射中心发射,2011年11月3日凌晨顺利实现与“神州八号”飞船的对接任务.某同学画出“天宫一号”和“神州八号”绕地球做匀速圆周运动的情境图,如图所示.图中A代表“天宫一号”,B代表“神州八号”,虚线为各自的轨道,由图可以判定( )
“天宫一号”(Tiangong-1)是中国第一个目标飞行器,于2011年9月29日21时16分3秒在酒泉卫星发射中心发射,2011年11月3日凌晨顺利实现与“神州八号”飞船的对接任务.某同学画出“天宫一号”和“神州八号”绕地球做匀速圆周运动的情境图,如图所示.图中A代表“天宫一号”,B代表“神州八号”,虚线为各自的轨道,由图可以判定( )
 “天宫一号”(Tiangong-1)是中国第一个目标飞行器,于2011年9月29日21时16分3秒在酒泉卫星发射中心发射,2011年11月3日凌晨顺利实现与“神州八号”飞船的对接任务.某同学画出“天宫一号”和“神州八号”绕地球做匀速圆周运动的情境图,如图所示.图中A代表“天宫一号”,B代表“神州八号”,虚线为各自的轨道,由图可以判定( )
“天宫一号”(Tiangong-1)是中国第一个目标飞行器,于2011年9月29日21时16分3秒在酒泉卫星发射中心发射,2011年11月3日凌晨顺利实现与“神州八号”飞船的对接任务.某同学画出“天宫一号”和“神州八号”绕地球做匀速圆周运动的情境图,如图所示.图中A代表“天宫一号”,B代表“神州八号”,虚线为各自的轨道,由图可以判定( )| A. | “天宫一号”的运行速率一定大于7.9km/s | |
| B. | “天宫一号”的周期一定小于“神州八号”的周期 | |
| C. | “神州八号”需通过适度的加速才能与“天宫一号”实现对接 | |
| D. | “天宫一号”的向心加速度一定大于“神州八号”的向心加速度 |

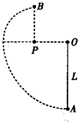 如图所示,一质量为m的小球用长为L的轻质细线悬于O点,与O点处于同一水平线上的P点处有一个光滑的细钉,OP=$\frac{L}{2}$,在A点给小球一个水平向左的初速度,发现小球恰能到达跟P点在同一竖直线上的最高点B,已知重力加速度为g,(设小球在运动过程中细线不会被拉断)
如图所示,一质量为m的小球用长为L的轻质细线悬于O点,与O点处于同一水平线上的P点处有一个光滑的细钉,OP=$\frac{L}{2}$,在A点给小球一个水平向左的初速度,发现小球恰能到达跟P点在同一竖直线上的最高点B,已知重力加速度为g,(设小球在运动过程中细线不会被拉断)