题目内容
【题目】A、B两球沿一直线运动并发生正碰，如图所示为两球碰撞前后的位移时间图象．a、b分别为A、B两球碰前的位移图象，C为碰撞后两球共同运动的位移图象，若A球质量是m=2kg，则由图象判断下列结论正确的是（）
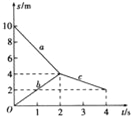
A. A、B碰撞前的总动量为3kgm/s B. 碰撞时A对B所施冲量为﹣4Ns
C. 碰撞前后A的动量变化为4kgm/s D. 碰撞中A、B两球组成的系统损失的动能为10J
【答案】A
【解析】由s-t图象可知，碰撞前有： 
， 
，碰撞后有：vA′=vB′=v= 
；对A、B组成的系统，A、B两球沿一直线运动并发生正碰，碰撞前后物体都是做匀速直线运动，所以系统的动量守恒．碰撞前后A的动量变化为：△PA=mvA′-mvA=2×（-1）-2×（-3）=4kgm/s，根据动量守恒定律，碰撞前后A的动量变化为：△PB=-△PA=-4kgm/s，又：△PB=mB（vB′-vB），所以： 
，
所以A与B碰撞前的总动量为：p总=mvA+mBvB=2×（-3）+
×2=-
kgm/s; 由动量定理可知，碰撞时A对B所施冲量为：IB=△PB=-4kgm/s=-4Ns．碰撞中A、B两球组成的系统损失的动能：△EK=
mvA2+
mBvB2-
（m+mB）v2，代入数据解得：△EK=10J，故A错误，BCD正确；故选BCD．
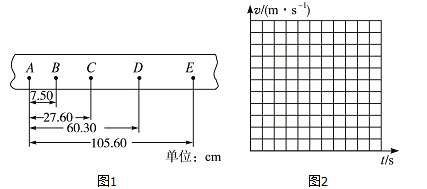
【题目】利用如图1所示的实验装置探究恒力做功与物体动能变化的关系．小车的质量为M=200.0g，钩码的质量为m=10.0g，打点计时器的电源为50Hz的交流电．
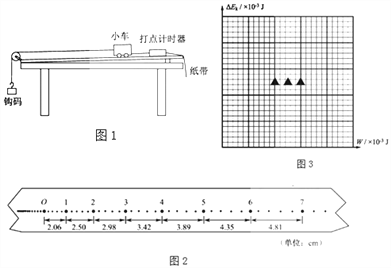
（1）挂钩码前，为了消除摩擦力的影响，应调节木板右侧的高度，直至向左轻推小车观察到_____．
（2）挂上钩码，按实验要求打出的一条纸带如图2所示．选择某一点为O，一次每隔4个计时点取一个计数点．用刻度尺量出相邻计数点间的距离△x，记录在纸带上．计算打出各计数点时小车的速度v，其中打出计数点“1”时小车的速度v1=_____m/s．
（3）将钩码的重力视位小车受到的拉力，取g=9.80m/s2，利用W=mg△x算出拉力对小车做的功W．利用Ek=
Mv2算出小车动能，并求出动能的变化量△Ek．计算结果见下表．
W/×10﹣3J | 2.45 | 2.92 | 3.35 | 3.81 | 4.26 |
△Ek/×10﹣3J | 2.31 | 2.73 | 3.12 | 3.61 | 4.00 |
请根据表中的数据，在答题卡的方格纸上作出△Ek﹣W图象．
（4）实验结果表明，△Ek总是略小于W．某同学猜想是由于小车所受拉力小于钩码重力造成的．用题中小车和钩码质量的数据可算出小车受到的实际拉力F=_____．
