题目内容
空间存在垂直于纸面方向的均匀磁场其方向随时间作周期性变化,磁感应强度B随时间t变化的图线如图(甲)所示.规定B>0时,磁场方向垂直纸面向外.现在磁场区域中建立一与磁场方向垂直的平面直角坐标系xoy,如图(乙)所示.一电量q=5π×10-7C质量m=5×10-10kg的带正电粒子,位于原点O处,在t=0时刻以初速度v0=πm/s沿x轴正方向开始运动,不计重力作用,不计磁场变化可能产生的一切其他影响.试求:

(1)带电粒子的运动半径;
(2)带电粒子从O点运动到P(4,4)点的最短时间;
(3)要使带电粒子过图中的P点,则磁场的变化周期T为多少?

(1)带电粒子的运动半径;
(2)带电粒子从O点运动到P(4,4)点的最短时间;
(3)要使带电粒子过图中的P点,则磁场的变化周期T为多少?
分析:(1)粒子在磁场中运动,洛伦兹力提供向心力,由牛顿第二定律可求出粒子运动轨迹的半径.
(2)由带电粒子在匀强磁场中的周期公式T=
可求出粒子的运动周期,通过题意找出磁场的变化周期和粒子的运动周期的关系,结合几何图形,可求出粒子到达P点的最短时间.
(3)结合第二问的分析,考虑到带电粒子从O到P运动中可完成的周期的重复性,列式求解即可.
(2)由带电粒子在匀强磁场中的周期公式T=
| 2πm |
| qB |
(3)结合第二问的分析,考虑到带电粒子从O到P运动中可完成的周期的重复性,列式求解即可.
解答:解:
(1)设粒子运动半径为R,则有
qvB=m
得:R=
=0.01m
(2)设点电粒子的运动周期为T粒,则:
T粒=
=0.02s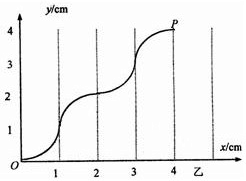
若磁场的变化周期T的
恰好为带电粒子运动周期T粒的
,即它的轨迹为4个
圆相连接,它的运动轨迹如图所示,此种情况带点粒子从O点运动到P点所用的时间最短,设为t,则:
t=T粒=0.02s
(3)要使带电粒子经过P点,则磁场变化的周期T和带电粒子在磁场中的运动周期T粒之间应满足的关系为:
=(n+
)T粒
即:T=0.04×(n+
)s n=0,1,2,3…
答:(1)带电粒子的运动半径为0.01m;
(2)带电粒子从O点运动到P(4,4)点的最短时间为0.02s
(3)要使带电粒子过图中的P点,则磁场的变化周期T为0.04×(n+
)s n=0,1,2,3…
(1)设粒子运动半径为R,则有
qvB=m
| v2 |
| R |
得:R=
| mv |
| qB |
(2)设点电粒子的运动周期为T粒,则:
T粒=
| 2πm |
| qB |

若磁场的变化周期T的
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
t=T粒=0.02s
(3)要使带电粒子经过P点,则磁场变化的周期T和带电粒子在磁场中的运动周期T粒之间应满足的关系为:
| T |
| 2 |
| 1 |
| 4 |
即:T=0.04×(n+
| 1 |
| 4 |
答:(1)带电粒子的运动半径为0.01m;
(2)带电粒子从O点运动到P(4,4)点的最短时间为0.02s
(3)要使带电粒子过图中的P点,则磁场的变化周期T为0.04×(n+
| 1 |
| 4 |
点评:该题考察了带电粒子在方向随时间作周期性变化的磁场中运动的问题,此题不但要求学生要熟练的应用带电粒子在匀强磁场中做圆周运动的轨道半径公式和周期公式,还要求要有较强的对物体运动的分析能力,该题关键是找出磁场变化的周期和粒子圆周运动的周期的关系.正确的绘制出粒子的轨迹图,对解决问题有非常大的帮助.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 (2006?德州一模)在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4kg、电荷量q=+9.0×10-4C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,sin37°=0.6,不计空气阻力,求:
(2006?德州一模)在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4kg、电荷量q=+9.0×10-4C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,sin37°=0.6,不计空气阻力,求: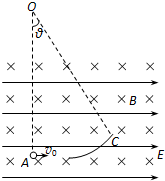 在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4 kg、电荷量q=+9.0×10-4 C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,求:
在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4 kg、电荷量q=+9.0×10-4 C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,求: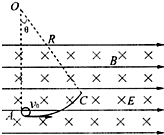 在某空间存在着水平向右的匀强电场E和垂直于纸面向里的匀强磁场B,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4kg、电荷量q=+9.0×10-4C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,求:
在某空间存在着水平向右的匀强电场E和垂直于纸面向里的匀强磁场B,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4kg、电荷量q=+9.0×10-4C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,求: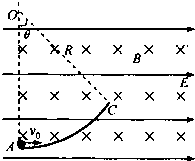 在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=370.现有一质量m=3.6×10-4kg电荷量q=+9.0×10-4C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,沿圆弧轨道运动并从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,
在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=370.现有一质量m=3.6×10-4kg电荷量q=+9.0×10-4C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,沿圆弧轨道运动并从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,