题目内容
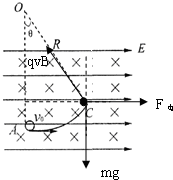
 (2006?德州一模)在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4kg、电荷量q=+9.0×10-4C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,sin37°=0.6,不计空气阻力,求:
(2006?德州一模)在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R=1.8m,OA连线在竖直方向上,AC弧对应的圆心角θ=37°.今有一质量m=3.6×10-4kg、电荷量q=+9.0×10-4C的带电小球(可视为质点),以v0=4.0m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动.已知重力加速度g=10m/s2,sin37°=0.6,不计空气阻力,求:(1)匀强电场的场强E;
(2)小球射入圆弧轨道后的瞬间对轨道的压力.
分析:(1)根据小球离开C点时处于平衡状态列平衡方程可正确求解;
(2)根据动能定理求出小球刚进入磁场时的速度大小,从而进一步求出磁场强度,在最低点进行受力分析,根据向心力公式列方程可正确求解.
(2)根据动能定理求出小球刚进入磁场时的速度大小,从而进一步求出磁场强度,在最低点进行受力分析,根据向心力公式列方程可正确求解.
解答:解:(1)当小球离开圆弧轨道后,对其受力分析如图所示:
由平衡条件得:F电=qE=mgtanθ
代入数据解得:E=3N/C
答:匀强电场的场强为:E=3N/C.
(2)小球从进入圆弧轨道到离开圆弧轨道的过程中,由动能定理得:
F电Rsinθ-mgR(1-cosθ)=
-
代入数据得:v=5m/s
由F 磁=qvB=
解得:B=1T
分析小球射入圆弧轨道瞬间的受力情况如图所示:
由牛顿第二定律得:F N=Bqvo-mg=
代入数据得:FN=3.2×10-3 N
由牛顿第三定律得,小球对轨道的压力为:FN=3.2×10-3 N
答:小球射入圆弧轨道后的瞬间对轨道的压力为:FN=3.2×10-3 N.

由平衡条件得:F电=qE=mgtanθ
代入数据解得:E=3N/C
答:匀强电场的场强为:E=3N/C.
(2)小球从进入圆弧轨道到离开圆弧轨道的过程中,由动能定理得:
F电Rsinθ-mgR(1-cosθ)=
| mv2 |
| 2 |
m
| ||
| 2 |
代入数据得:v=5m/s
由F 磁=qvB=
| mg |
| cosθ |
解得:B=1T
分析小球射入圆弧轨道瞬间的受力情况如图所示:
由牛顿第二定律得:F N=Bqvo-mg=
m
| ||
| R |
代入数据得:FN=3.2×10-3 N
由牛顿第三定律得,小球对轨道的压力为:FN=3.2×10-3 N
答:小球射入圆弧轨道后的瞬间对轨道的压力为:FN=3.2×10-3 N.
点评:本题考查了带电粒子在复合场中的运动,对于这类问题关键是正确进行受力分力,明确运动形式,根据相关规律解答.

练习册系列答案
相关题目
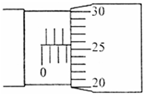 (2006?德州一模)某同学用螺旋测微器测定一金属丝的直径,测得的结果如图所示,则该金属丝的直径d=
(2006?德州一模)某同学用螺旋测微器测定一金属丝的直径,测得的结果如图所示,则该金属丝的直径d=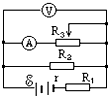 (2006?德州一模)如图所示,当滑动变阻器的滑动片向右移动时,各电表读数的变化情况是( )
(2006?德州一模)如图所示,当滑动变阻器的滑动片向右移动时,各电表读数的变化情况是( )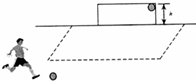 (2006?德州一模)在足球比赛中,甲队队员在乙队禁区附近主罚定位球,并将球从球门右上角贴着门射入,如图所示,已知球门高度为h,足球飞入球门时的速度为v,足球质量为m,不计空气阻力和足球的大小,则该队员对足球的做功为( )
(2006?德州一模)在足球比赛中,甲队队员在乙队禁区附近主罚定位球,并将球从球门右上角贴着门射入,如图所示,已知球门高度为h,足球飞入球门时的速度为v,足球质量为m,不计空气阻力和足球的大小,则该队员对足球的做功为( )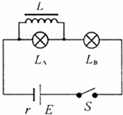 (2006?德州一模)如图所示的电路中,电感线圈L的自感系数足够大,其直流电阻忽略不计,LA、LB是两个相同的灯泡,下列说法下确的是( )
(2006?德州一模)如图所示的电路中,电感线圈L的自感系数足够大,其直流电阻忽略不计,LA、LB是两个相同的灯泡,下列说法下确的是( )