题目内容
 如图所示,在长为L的细绳y端系一个质量为m的小球A,小球绕绳的另一固定端O点在竖直平面内做圆周运动,如果小球经过最高点时,绳对小球的拉力大小等于小球的重力,求:
如图所示,在长为L的细绳y端系一个质量为m的小球A,小球绕绳的另一固定端O点在竖直平面内做圆周运动,如果小球经过最高点时,绳对小球的拉力大小等于小球的重力,求:(1)小球经过最高点时的速度大小;
(2)小球经过最低点时的速度大小;
(3)小球经过最低点时绳对球的拉力大小.
分析:(1)根据小球在最高点的拉力,结合牛顿第二定律求出小球经过最高点的速度大小.
(2)根据机械能守恒定律求出小球经过最低点时的速度大小.
(3)在最低点靠拉力和重力的合力提供向心力,根据牛顿第二定律求出拉力的大小.
(2)根据机械能守恒定律求出小球经过最低点时的速度大小.
(3)在最低点靠拉力和重力的合力提供向心力,根据牛顿第二定律求出拉力的大小.
解答:解:(1)在最高点,拉力F=mg
根据牛顿第二定律得,F+mg=m
解得v1=
.
(2)根据机械能守恒定律得,
mv12+mg2L=
mv22
代入数据解得,v2=
.
(3)根据牛顿第二定律得,F′-mg=m
解得F′=7mg.
答:(1)小球经过最高点时的速度大小v1=
.
(2)小球经过最低点时的速度大小
.
(3)小球经过最低点时绳对球的拉力大小为7mg.
根据牛顿第二定律得,F+mg=m
| v12 |
| L |
解得v1=
| 2gL |
(2)根据机械能守恒定律得,
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得,v2=
| 6gL |
(3)根据牛顿第二定律得,F′-mg=m
| v22 |
| L |
解得F′=7mg.
答:(1)小球经过最高点时的速度大小v1=
| 2gL |
(2)小球经过最低点时的速度大小
| 6gL |
(3)小球经过最低点时绳对球的拉力大小为7mg.
点评:本题考查牛顿第二定律和机械能守恒定律的综合,知道圆周运动向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
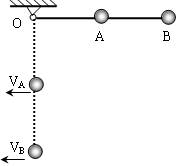
 如图所示,在长为L的轻杆中点A和端点B各固定一质量均为m的小球,杆可绕无摩擦的轴O转动,使杆从水平位置无初速释放摆下.求当杆转到竖直位置时,轻杆对A、B两球分别做了多少功?
如图所示,在长为L的轻杆中点A和端点B各固定一质量均为m的小球,杆可绕无摩擦的轴O转动,使杆从水平位置无初速释放摆下.求当杆转到竖直位置时,轻杆对A、B两球分别做了多少功?