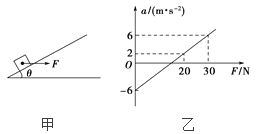
��Ŀ����
����Ŀ����ͼ��ʾ����E=103V/m��ˮƽ������ǿ�糡�У���һ�⻬��Բ�ξ�Ե�����ֱ���ã������һˮƽ��Ե���MN���ӣ���Բ���������ֱƽ����糡��ƽ�У���뾶R=40cm��һ�������q=10��4C��С��������Ϊm=40g����ˮƽ�����Ķ�Ħ����m=0.2��ȡg=10m/s2����
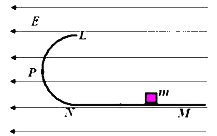
��1��ҪС�������˶���Բ�������ߵ�L������Ӧ��ˮƽ�������N���Զ���ͷţ�
��2�������ͷŵĻ���ͨ��P��ʱ�Թ��ѹ���Ƕ��PΪ��Բ����е㣩
���𰸡���1��20cm��2��1.5N
�������������������С�����˶��Ĺ����У�Ħ�����Ի�����������������糡���Ի��������������ݶ��ܶ���������û�����N��֮��ľ��룻��P��ʱ���Ի���������������ţ�ٵڶ����ɿ�����û����ܵ��Ĺ���Ի����֧�����Ĵ�С����ţ�ٵ������ɿ�����öԹ��ѹ����
��1���軬����N��ľ���ΪL��
����������˶����̣��ɶ��ܶ����ɵã� ![]()
С������D��ʱ�������ṩ������������![]()
�������ݽ��![]() ��
��
��2�����鵽��P��ʱ����ȫ����Ӧ�ö��ܶ����ɵã� ![]()
��P��ʱ��ţ�ٵڶ����ɿɵ�![]() �����
�����![]()
��ţ�ٵ������ɿɵã�����ͨ��P��ʱ�Թ��ѹ����1.5N��

��ϰ��ϵ�д�
�����Ŀ