题目内容

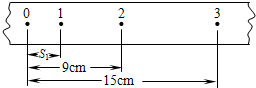在做“测定匀变速直线运动的加速度”的实验中，取下一段纸带研究其运动情况，如图所示．设0点为计数的起始点，相邻两计数点间的时间间隔为0.1s，若物体做理想的匀加速直线运动，则计数点“1”与起始点间的距离s1为
4.00
4.00
cm，物体的加速度为
1.00
1.00
m/s2．（结果均保留3位有效数字）
分析：由匀变速直线运动的推论△s=aT2可以A与起始点O之间的距离，
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小．
解答：解：根据匀变速直线运动的特点（相邻的时间间隔位移之差相等）得出：
x23-x12=x12-x01
计数点1与起始点0之间的距离s1为4.00cm
根据运动学公式△x=at2得：
a=
x12-x01
T2
=
0.05-0.04
(0.1)2
=1.00m/s2，
故答案为：4.00，1.00
点评：要提高应用匀变速直线的规律以及推论解答实验问题的能力，在平时练习中要加强基础知识的理解与应用．
练习册系列答案
相关题目
某同学在做“测定匀变速直线运动的加速度”实验时，从打下的若干纸带中选出了如图所示的一条（每两点间还有4个点没有画出来），图中上部的数字为相邻两个计数点间的距离．打点计时器的电源频率为50Hz．由这些已知数据计算：①该匀变速直线运动的加速度a=
1.93
1.93
m/s2．②与纸带上D点相对应的瞬时速度v=
1.18
1.18
 m/s．（答案均要求保留3位有效数字）
（1）打点计时器的正常工作频率是50Hz，但在做“测定匀变速直线运动加速度”的实验时，一同学不知道他的打点计时器的实际频率小于50Hz，那么他计算出的加速度的值与正常情况下的测量值相比将
偏大
偏大
．（填“偏大、偏小或不变”）
（2）下面是一同学在做“测定匀变速直线运动加速度”的实验时得到的实验纸带的一部分，A、B、C、D、E是按时间顺序的相邻的记数点，并且在相邻的记数点之间还有4个点未标出，纸带上A、B、C、D离E点的距离分别是49.00cm，31.50cm，17.50cm和7.00cm，则实验中小车做
匀减速
匀减速
直线运动（填“匀加速”或“匀减速”），加速度大小为
3.50m/s2
3.50m/s2
，C点的瞬时速度为
1.23
1.23
，方向向
右
右
．（结果保留3位有效数字）
（1）图1为“探究求合力的方法”的实验装置．

①下列说法中正确的是
AC
AC

A．在测量同一组数据F1、F2和合力F的过程中，橡皮条结点O的位置不能变化
B．弹簧测力计拉细线时，拉力方向必须竖直向下
C．F1、F2和合力F的大小都不能超过弹簧测力计的量程
D．为减小测量误差，F1、F2方向间夹角应为90°
②弹簧测力计的指针如图2所示，由图2可知拉力的大小为
4.0
4.0
 N．
（2）某同学在做“测定匀变速直线运动的加速度”实验时，从打下的若干纸带中选出了如图3所示的一条（每两点间还有4个点没有画出来），图中上部的数字为相邻两个计数点间的距离．打点计时器的电源频率为50Hz．由这些已知数据计算：①该匀变速直线运动的加速度a=
1.93
1.93
m/s2．②与纸带上D点相对应的瞬时速度v=
1.18
1.18
 m/s．（答案均要求保留3位有效数字）
（1）某同学在做“测定匀变速直线运动的加速度”实验时，从打下的若干纸带中选出了如图所示的一条（每两点间还有4个点没有画出来），图中上部的数字为相邻两个计数点间的距离．打点计时器的电源频率为50Hz．由这些已知数据计算：

①该匀变速直线运动的加速度a=
2.05
2.05
m/s2．
②与纸带上D点相对应的瞬时速度v=
1.22
1.22
 m/s．（保留3位有效数字）
（2）为了测量一个高楼的高度，某同学设计了如下实验：在一根长为l的绳两端各拴一重球，一人站在楼顶上，手执上端的重球无初速度的释放使其自由下落，另一人在楼下测量两球落地的时间差△t，即可根据l、△t、g得出高楼的高度（不计空气阻力）．
①从原理说明此方案是否可行及理由
可行，h=
1
2
gt2，h+L=
1
2
g（t+△t）2，两个方程，两个未知数，方程可解
可行，h=
1
2
gt2，h+L=
1
2
g（t+△t）2，两个方程，两个未知数，方程可解
．②从实际测量来看，你估计最大的困难是
△t太小，难以测量
△t太小，难以测量

（3）某同学在做测定木板的动摩擦因数的实验时，设计了两种方案．
方案A：木板水平固定，通过弹簧秤水平拉动木块，如图a；
方案B：木块固定，通过细线水平拉动木板，如图b．
上述两方案中，你认为更合理的是
b
b
，该实验中需要测量的物理量是
弹簧秤示数F和木块的重量G
弹簧秤示数F和木块的重量G
．
（1）在做“测定匀变速直线运动的加速度”的实验中，取下一段纸带研究其运动情况，如图1所示．设0点为计数的起始点，相邻两计数点间的时间间隔为0.1s，若物体做理想的匀加速直线运动，则计数点“1”与起始点间的距离s1为
4.00
4.00
cm，打计数点“1”时物体的瞬时速度为
0.450
0.450
m/s，物体的加速度为
1.00
1.00
m/s2．（结果均保留3位有效数字）
（2）将一单摆装置竖直悬于某一深度为h（未知）且开口向下的固定小筒中（单摆的下部分露出筒外），如图甲所示．将悬线拉离平衡位置一个小角度后由静止释放，设单摆摆动过程中悬线不会碰到筒壁．如果本实验的长度测量工具只能测量出筒下端口到摆球球心之间的距离L，并通过改变L而测出对应的摆动周期T，再以T2为纵轴、L为横轴，作出T2-L图象，则可以由此图象得出小筒的深度h和当地的重力加速度g．
①如果实验中所得到的T2-L图象如图乙所示，那么对应的图象应该是a、b、c中的
a
a
．
②由图象可知，小筒的深度h=
0.3
0.3
m；当地重力加速度g=
9.86
9.86
m/s2（结果均保留3位有效数字）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网