Question

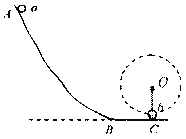
【题目】如图所示，小球b静止与光滑水平面BC上的C点，被长为L的细线悬挂于O点，细绳拉直但张力为零．小球a从光滑曲面轨道上AB上的B点由静止释放，沿轨道滑下后，进入水平面BC（不计小球在B处的能量损失），与小球b发生正碰，碰后两球粘在一起，在细绳的作 用下在竖直面内做圆周运动且恰好通过最高点．已知小球a的质景为M，小球b的质量为m．M=5m．己知当地重力加速度为g求：

（1）小球a与b碰后的瞬时速度大小

（2）A点与水平面BC间的高度差．

Answer 1

【答案】（1）（2）3.6L

【解析】解：（1）两球恰能到达圆周最高点时，重力提供向心力，

由牛顿第二定律得：（m+M）g=（m+M），

从碰撞后到最高点过程，由动能定理得：

﹣（M+m）g2L=（M+m）v2﹣（M+m）v共2，

解得，两球碰撞后的瞬时速度：v共=；

（2）设两球碰前a球速度为va，两球碰撞过程动量守恒，

以向右为正方向，由动量守恒定律得：Mva=（M+m）v共，

解得：va=，

a球从A点下滑到C点过程中，由机械能守恒定律得：

Mgh=Mva2，解得：h=3.6L；