题目内容
15．从某一高度相隔1s先后释放两个相同的小球甲和乙，不计空气的阻力，它们在空中任一时刻（ ）| A． | 甲、乙两球距离始终保持不变，甲、乙两球速度之差保持不变 | |
| B． | 甲、乙两球距离越来越大，甲、乙两球速度之差也越来越大 | |
| C． | 甲、乙两球距离越来越小，甲、乙两球速度之差也越来越小 | |
| D． | 甲、乙两球距离越来越大，甲、乙两球速度之差保持不变 |
分析 甲、乙两球均做自由落体运动，由位移公式列出它们的距离与时间关系的表达式，再求出速度之差与时间的关系式．
解答 解：以释放第2个球开始计时，第一个球此时的速度v1=gt=10m/s，与第二球之间的距离x1=$\frac{1}{2}g{t}^{2}=\frac{1}{2}×10×1m=5m$，经过t时间后，第一个球的位移x=v1t$+\frac{1}{2}g{t}^{2}$，第二个球的位移x′=$\frac{1}{2}g{t}^{2}$，△x=5+v1t，知两球的距离越来越大．
以释放第2个球开始计时，第一个球此时的速度v1=gt=10m/s，经过t时间后，第一个球的速度v=v1+gt，第二个球的速度v′=gt，则两球的速度差△v=v-v′=10m/s．两球的速度之差保持不变，故ABC错误，D正确；
故选：D
点评 本题可以通过匀变速直线运动的速度时间公式和位移时间公式求出两球间的距离和两球的速度之差，判断其如何变化．本题也可以以释放的第二个球为参考系，第一个球做匀速直线运动，从而可以判断出两球距离和速度之差的变化．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
5．
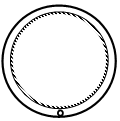如图所示，在竖直平面内固定有两个很靠近的同心圆轨道，外圆光滑，内圆粗糙．一质量为m的小球从轨道的最低点以初速度v0向右运动，球的直径略小于两圆间距，球运动的轨道半径为R，不计空气阻力．设小球过最低点时重力势能为零，下列说法正确的是（ ）
如图所示，在竖直平面内固定有两个很靠近的同心圆轨道，外圆光滑，内圆粗糙．一质量为m的小球从轨道的最低点以初速度v0向右运动，球的直径略小于两圆间距，球运动的轨道半径为R，不计空气阻力．设小球过最低点时重力势能为零，下列说法正确的是（ ）| A． | 若小球运动到最高点时速度为0，则小球机械能一定不守恒 | |
| B． | 若经过足够长时间，小球最终的机械能可能为$\frac{3}{2}$mgR | |
| C． | 若使小球始终做完整的圆周运动，则v0一定不小于$\sqrt{5gR}$ | |
| D． | 若小球第一次运动到最高点时速度大小为0，则v0一定大于$\sqrt{4gR}$ |
3．关于质点，下列说法不正确的是（ ）
| A． | 研究运动员的运动时，运动员不能看作质点 | |
| B． | 物体能否看作质点，不能由体积的大小来判断 | |
| C． | 研究月相时，可以把月球视为质点 | |
| D． | 物体能否看作质点，不能由质量的大小来判断 |
20．沿直线运动的一列火车和一辆汽车在开始计时及每过1s的速度分别为v1和v2，如下表所示，从表中数据可以看出（ ）
| t/s | 0 | 1 | 2 | 3 | 4 | 5 |
| 火车 | v1/m•s-1 | 18.0 | 17.5 | 17.0 | 16.5 | 16.0 |
| 汽车 | v2/m•s-1 | 9.8 | 11.0 | 12.2 | 13.4 | 14.6 |
| A． | 火车的速度变化较慢 | B． | 汽车的加速度较大 | ||
| C． | 火车的位移在减小 | D． | 汽车的位移在增大 |
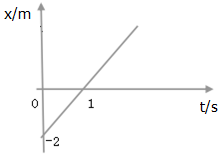
7．
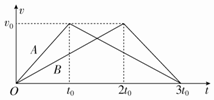质量分别为2m和m的A、B两种物体分别在水平恒力F1和F2的作用下沿水平面运动，撤去F1、F2后受摩擦力的作用减速到停止，其vt图象如图所示，则下列说法正确的是（ ）
质量分别为2m和m的A、B两种物体分别在水平恒力F1和F2的作用下沿水平面运动，撤去F1、F2后受摩擦力的作用减速到停止，其vt图象如图所示，则下列说法正确的是（ ）| A． | F1、F2大小之比为1：1 | |
| B． | F1、F2对A、B做功之比为1：1 | |
| C． | A、B受到的摩擦力大小之比为1：1 | |
| D． | 全过程中摩擦力对A、B做功之比为1：2 |
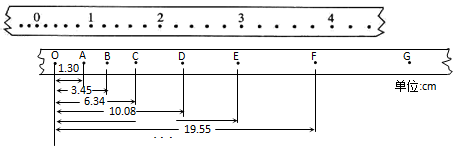
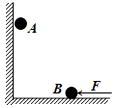如图所示，竖直墙面与水平地面均光滑且绝缘，两个带有同种电荷的小球A、B分别处于竖直墙面和水平地面，且处于同一竖直平面内，若用图示方向的水平推力F作用于小球B，则两球静止于图示位置．如果将小球向左推动少许，并待两球重新达到平衡时，跟原来的状态相比，竖直墙面对小球A的推力变小；地面对小球B的支持力不变；两小球之间的距离变大．（填“变大”、“变小”或“不变”）