Question

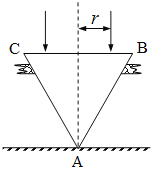
【题目】在桌面上有一倒立的玻璃圆锥，其顶点恰好与桌面接触，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面是边长为a的等边三角形，如图所示．有一半径为r的圆柱形平行光束垂直入射到圆锥的地面上，光束的中心轴与圆锥的轴重合．已知玻璃的折射率为，光在空气中传播的速度为c.求：

（1）光束在桌面上形成的光斑半径R

（2）光束在玻璃中传播的时间t

Answer 1

【答案】（1）R=2r（2）

【解析】

平行光束垂直入射到圆锥的底面上，方向不变射到母线上发生折射，由于入射角等于60°，而玻璃的折射率为1.5，可得临界角小于45°，所以会发生光的全反射，反射光线却恰好垂直射出．故可根据几何关系可确定光斑的半径光束在桌面上形成的光斑半径R；根据几何知识求光束在玻璃中传播的距离，由求出光束在玻璃中传播的速度，从而求得光束在玻璃中传播的时间t．

（i）设玻璃的临界角为C，根据①，得②；

光线垂直圆锥底面BC射入玻璃时，直线传到AB面．由几何关系可知入射角 ，

由于，所以光线会在AB面上发生全反射③，

光路如图，由几何关系知，反射光线恰好垂直AC面射出④，

由几何关系可知：AE=2r，在△AEG中，由于∠AEG=∠AGE=30°，则AG=AE=2r⑤，

所以，由旋转对称性可知光束在桌面上形成的光斑半径R=2r⑥；

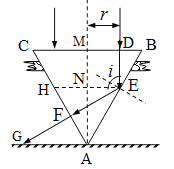
（ii）由于△AEH为等边三角形，所以EF=AN，

故光线在玻璃中的传播距离始终为⑦，

其余入射点的光线在玻璃中的传播距离类似证明均为L，
光线在玻璃中的传播时间⑧，而⑨，

联立解得⑩；

另解：（ii）如图，经过任意入射点P的光线在玻璃中的传播传播路径为PQS，由于△AQT为等边三角形，所以QS=AJ，

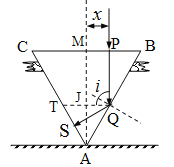
故光线在玻璃中的传播距离始终为⑦
光线在玻璃中的传播时间⑧，而⑨，

联立解得⑩