题目内容
14.如图甲所示,足够长的木板B静置于光滑水平面上,其上放置小滑块A.木板B受到随时间t变化的水平拉力F作用时,用传感器测出木板B的加速度a,得到如图乙所示的a-F图象,已知g取10m/s2,则( )
| A. | 滑块A的质量为4kg | B. | 木板B的质量为1kg | ||
| C. | 当F=10N时木板B加速度为4m/s2 | D. | 滑块A与木板B间动摩擦因数为0.1 |
分析 当拉力较小时,m和M保持相对静止一起做匀加速直线运动,当拉力达到一定值时,m和M发生相对滑动,结合牛顿第二定律,运用整体和隔离法进行解答.
解答 解:ABD、由图知,当F=8N时,加速度为:a=2m/s2,对整体分析,由牛顿第二定律有:F=(mA+mB)a,代入数据解得:mA+mB=4kg,当F大于8N时,A、B发生相对滑动,根据牛顿第二定律得:对B有:a=$\frac{F-μ{m}_{A}g}{{m}_{B}}$=$\frac{1}{{m}_{B}}$F-$\frac{μ{m}_{A}g}{{m}_{B}}$,由图示图象可知,图线的斜率:k=$\frac{1}{{m}_{B}}$=$\frac{△a}{△F}$=$\frac{2}{8-6}$=1,解得:mB=1kg,滑块A的质量为:mA=3kg.
当a=0时,F=6N,代入解得 μ=0.2,故A、D错误,B正确.
C、根据F=10N>8N时,滑块与木板相对滑动,B的加速度为:aB=a=$\frac{F-μ{m}_{A}g}{{m}_{B}}$=$\frac{1}{{m}_{B}}$F-μg=$\frac{1}{1}×10$-$\frac{0.2×30}{1}$=4m/s2.故C正确.
故选:BC
点评 本题考查牛顿第二定律与图象的综合,知道滑块和木板在不同拉力作用下的运动规律是解决本题的关键,掌握处理图象问题的一般方法,通常通过图线的斜率和截距入手分析.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5. 为了让乘客乘车更为舒适,某探究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使得座椅始终保持水平,当此车上坡时,( )
为了让乘客乘车更为舒适,某探究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使得座椅始终保持水平,当此车上坡时,( )
 为了让乘客乘车更为舒适,某探究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使得座椅始终保持水平,当此车上坡时,( )
为了让乘客乘车更为舒适,某探究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使得座椅始终保持水平,当此车上坡时,( )| A. | 当匀速上坡时,乘客受到的支持力大于重力 | |
| B. | 当加速上坡时,乘客受到的支持力大于重力 | |
| C. | 当匀速上坡时,乘客受到的摩擦力向右 | |
| D. | 当加速上坡时,乘客受到的摩擦力向右 |
19. 图甲是法拉第发明的人类历史上的第一台发电机,图乙是这个圆盘发电机的示意图:圆盘安装在水平铜轴上,它的边缘正好在两磁极之间,两块铜片C、D分别与转动轴和铜盘的边缘接触,下列分折正确的是( )
图甲是法拉第发明的人类历史上的第一台发电机,图乙是这个圆盘发电机的示意图:圆盘安装在水平铜轴上,它的边缘正好在两磁极之间,两块铜片C、D分别与转动轴和铜盘的边缘接触,下列分折正确的是( )
 图甲是法拉第发明的人类历史上的第一台发电机,图乙是这个圆盘发电机的示意图:圆盘安装在水平铜轴上,它的边缘正好在两磁极之间,两块铜片C、D分别与转动轴和铜盘的边缘接触,下列分折正确的是( )
图甲是法拉第发明的人类历史上的第一台发电机,图乙是这个圆盘发电机的示意图:圆盘安装在水平铜轴上,它的边缘正好在两磁极之间,两块铜片C、D分别与转动轴和铜盘的边缘接触,下列分折正确的是( )| A. | 因穿过铜盘的磁通量没有发生变化,故法拉第的第一台发电机不能发电 | |
| B. | 假若该发电机能发电,则图乙中R上的电流从下向上流动 | |
| C. | 图乙中流过R的是方向不断改变的交流电 | |
| D. | 设图乙中铜盘半径为r,匀强磁场大小为B,铜盘转动的角速度为ω,铜盘产生的电动势为E=Bωr2 |
6.图中为两个不同闭合电路中两个不同电源的U-I图象,下列判断正确的是( )


| A. | 电动势E1=E2,发生短路时的电流I1>I2 | |
| B. | 电动势E1=E2,内阻r1<r2 | |
| C. | 电动势E1>E2,内阻 r1<r2 | |
| D. | 当两电源的工作电流变化量相同时,电源2的路端电压变化大 |
3. 在“验证力的平行四边形定则”的实验中,某同学的实验情况如图甲所示,其中A为固定橡皮条的图钉,O为橡皮条与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的力的图示,下列说法中正确的是 ( )
在“验证力的平行四边形定则”的实验中,某同学的实验情况如图甲所示,其中A为固定橡皮条的图钉,O为橡皮条与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的力的图示,下列说法中正确的是 ( )
 在“验证力的平行四边形定则”的实验中,某同学的实验情况如图甲所示,其中A为固定橡皮条的图钉,O为橡皮条与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的力的图示,下列说法中正确的是 ( )
在“验证力的平行四边形定则”的实验中,某同学的实验情况如图甲所示,其中A为固定橡皮条的图钉,O为橡皮条与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的力的图示,下列说法中正确的是 ( )| A. | 图乙中的F是力F1和F2合力的真实值 | |
| B. | 图乙的F′是力F1和F2合力的真实值 | |
| C. | 在实验中,如果将细绳也换成橡皮条,那么对实验结果没有影响 | |
| D. | 在实验中,如果将细绳也换成橡皮条,那么对实验结果有影响 |
4. 如图所示,当光滑的斜面缓慢地沿水平地面向左推动过程中,绳对小球拉力T和斜面对小球支持力N变化情况是(小球半径不计)( )
如图所示,当光滑的斜面缓慢地沿水平地面向左推动过程中,绳对小球拉力T和斜面对小球支持力N变化情况是(小球半径不计)( )
 如图所示,当光滑的斜面缓慢地沿水平地面向左推动过程中,绳对小球拉力T和斜面对小球支持力N变化情况是(小球半径不计)( )
如图所示,当光滑的斜面缓慢地沿水平地面向左推动过程中,绳对小球拉力T和斜面对小球支持力N变化情况是(小球半径不计)( )| A. | T先变小后变大,N逐渐变大 | B. | T、N都逐渐变大 | ||
| C. | T、N都是先变大后变小 | D. | T逐渐变小,N逐渐变大 |
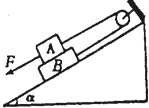 在图中所示的装置中,斜面倾角α=37°,A的质量是m1=10kg,A与B之间的动摩擦因数为μ1=0.1,B的质量为m2=20kg,B与斜面之间的动摩擦因数为μ2=0.2,为使B沿斜面向上匀速运动,应当用多大的力F沿斜面方向向下拉A?(g取10m/s2,sin37°=0.6,Cos37°=0.8)
在图中所示的装置中,斜面倾角α=37°,A的质量是m1=10kg,A与B之间的动摩擦因数为μ1=0.1,B的质量为m2=20kg,B与斜面之间的动摩擦因数为μ2=0.2,为使B沿斜面向上匀速运动,应当用多大的力F沿斜面方向向下拉A?(g取10m/s2,sin37°=0.6,Cos37°=0.8) 如图所示,足够长的平行玻璃砖厚度d=3$\sqrt{6}$cm,底面镀有反光膜,顶面嵌有涂有遮光物质的挡板AB.一束光线以i=45°的入射角由挡板的A端入射,经底面反射后,恰能从挡板的B端射出.已知光线在玻璃砖中的折射率n=$\sqrt{2}$,真空中的光速c=3×108m/s,求:
如图所示,足够长的平行玻璃砖厚度d=3$\sqrt{6}$cm,底面镀有反光膜,顶面嵌有涂有遮光物质的挡板AB.一束光线以i=45°的入射角由挡板的A端入射,经底面反射后,恰能从挡板的B端射出.已知光线在玻璃砖中的折射率n=$\sqrt{2}$,真空中的光速c=3×108m/s,求: 如图所示,重物用BC、AC、CD三根绳吊在天花板上,已知β=30°,α=60°,BC和AC所能承受的最大拉力均为100N,CD能承受的最大拉力为300N,若使三根绳均不断,则挂在下面的物体的重力不能超过多大?
如图所示,重物用BC、AC、CD三根绳吊在天花板上,已知β=30°,α=60°,BC和AC所能承受的最大拉力均为100N,CD能承受的最大拉力为300N,若使三根绳均不断,则挂在下面的物体的重力不能超过多大?