Question

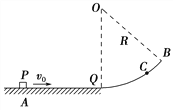
【题目】如图所示传送带A、B之间的距离为L=4m，与水平面间夹角θ=37°，传送带沿逆时针方向转动，速度恒为v=2m/s，在上端A点无初速放置一个质量为m=1kg、大小可视为质点的金属块，它与传送带的动摩擦因数为μ=0.5，金属块滑离传送带后，经过弯道，沿半径R=0.4m的光滑轨道做圆周运动，刚好能通过最高点E，已知B、D两点的竖直高度差为h=0.5m（取g=10m/s2，sin37°=0.6，cos37°=0.8）．求：

（1）金属块经过D点时的速度VD；

（2）金属块经过D点时受到的支持力FN

（3）金属块在BCD轨道上克服摩擦力做的功Wf．

Answer 1

【答案】（1） （2）60N（3）3J

【解析】（1）对金属块在E点，有：
代入数据解得：vE=2m/s
在从D到E过程中，由动能定理得：-mg2R=mvE2-mvD2
代入数据得：vD=2m/s；
（2）在D点根据牛顿第二定律可得： ，

解得FN=60N

（3）金属块在从A到D的过程中，由动能定理可知：
mg（Lsin37°+h）-WfBD-μmgLcos37°=mvD2-0
解得在BCD轨道上克服摩擦力做功 WfBD=3J；