题目内容
13.用铁锤将一铁钉击入木块,设木块对铁钉的阻力与铁钉进入木块内的深度成正比,在铁锤击打第一次后,能把铁钉击入木块内1cm,则击第二次后,能击入的深度为(设铁锤每次做功相等)( )| A. | 0.01cm | B. | 0.21cm | C. | 0.41cm | D. | 0.51cm |
分析 设铁钉进入木板的深度为d,所受的阻力大小为f,因为阻力与深度成正比,可以得到阻力的平均值,所以可以结合功的公式分析求解.
解答 解:设铁钉进入木板的深度为d,所受的阻力大小为f,由题意可知,f=kd
根据动能定理得:
第一次,铁锤做功:W1=$\frac{0+k{d}_{1}}{2}$•d1=$\frac{k{d}_{1}^{2}}{2}$
第二次,铁锤做功:W2=$\frac{k{d}_{1}+k{d}_{2}}{2}$•(d2-d1)
解得 d2=$\sqrt{2}$d1
所以第二次钉子进入木板的深度:h=d2-d1=($\sqrt{2}$-1)d1=(1.414-1)×0.01m≈0.00414m=0.41cm
故选:C.
点评 本题求变力做功时,要用其平均值,由于阻力与浓度成正比,所以平均阻力才等于初、末阻力的平均值.

练习册系列答案
相关题目
3.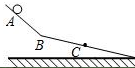 如图所示,两光滑斜面在B处连接,小球从A处由静止释放,经过B、C两点时速度大小分别是3m/s和4m/s,AB=BC.设球经过B点前后速度大小不变,则下列判断正确的是( )
如图所示,两光滑斜面在B处连接,小球从A处由静止释放,经过B、C两点时速度大小分别是3m/s和4m/s,AB=BC.设球经过B点前后速度大小不变,则下列判断正确的是( )
 如图所示,两光滑斜面在B处连接,小球从A处由静止释放,经过B、C两点时速度大小分别是3m/s和4m/s,AB=BC.设球经过B点前后速度大小不变,则下列判断正确的是( )
如图所示,两光滑斜面在B处连接,小球从A处由静止释放,经过B、C两点时速度大小分别是3m/s和4m/s,AB=BC.设球经过B点前后速度大小不变,则下列判断正确的是( )| A. | 球在AB、BC段的加速度大小之比为4:3 | |
| B. | 球由A运动到C的过程中平均速率为2.1m/s | |
| C. | 小球在AB、BC段的运动时间之比为7:4 | |
| D. | 小球从B运动到C过程中平均速度大小为3.5m/s |
4.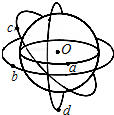 如图所示,a为放在赤道上随地球一起自转的物体,b为同步卫星,c为一般卫星,d为极地卫星.设b、c﹑d三卫星距地心的距离均为r,做匀速圆周运动.则下列说法正确的是( )
如图所示,a为放在赤道上随地球一起自转的物体,b为同步卫星,c为一般卫星,d为极地卫星.设b、c﹑d三卫星距地心的距离均为r,做匀速圆周运动.则下列说法正确的是( )
 如图所示,a为放在赤道上随地球一起自转的物体,b为同步卫星,c为一般卫星,d为极地卫星.设b、c﹑d三卫星距地心的距离均为r,做匀速圆周运动.则下列说法正确的是( )
如图所示,a为放在赤道上随地球一起自转的物体,b为同步卫星,c为一般卫星,d为极地卫星.设b、c﹑d三卫星距地心的距离均为r,做匀速圆周运动.则下列说法正确的是( )| A. | a、b﹑c﹑d线速度大小相等 | |
| B. | a、b﹑c﹑d角速度大小相等 | |
| C. | a、b﹑c﹑d向心加速度大小相等 | |
| D. | 若b卫星升到更高圆轨道上运动,则b仍可能与a物体相对静止 |
5.甲乙两个物体都做匀加速直线运动,从同一时刻开始计时的一段时间内,两物体的位移相等,则在这段时间内( )
| A. | 甲的初速度一定等于乙的初速度 | |
| B. | 甲的平均速度一定等于乙的平均速度 | |
| C. | 甲的速度变化量一定等于乙的速度变化量 | |
| D. | 甲的速度变化一定和乙的速度变化一样快 |
14.一个静止的原子核${\;}_{b}^{a}$X经α衰变放出一个α粒子并生成一个新核,α粒子的动能为E0.设衰变时产生的能量全部变成α粒子和新核的动能,则在此衰变过程中的质量亏损为( )
| A. | $\frac{{E}_{0}}{{c}^{2}}$ | B. | $\frac{{E}_{0}}{(a-4){c}^{2}}$ | C. | $\frac{(a-4){E}_{0}}{{c}^{2}}$ | D. | $\frac{a{E}_{0}}{(a-4){c}^{2}}$ |
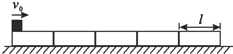 5个相同的木块紧挨着静止放在地面上,如图所示.每块木块的质量为m=1kg,长l=1m.它们与地面间的动摩擦因数μ1=0.1,木块与地面的最大静摩擦力等于滑动摩擦力.现有一质量为M=2.5kg的小铅块(视为质点),以v0=4m/s的初速度向右滑上左边第一木块的左端,它与木块的动摩擦因数μ2=0.2.小铅块刚滑到第四块木块时,木块开始运动,求:
5个相同的木块紧挨着静止放在地面上,如图所示.每块木块的质量为m=1kg,长l=1m.它们与地面间的动摩擦因数μ1=0.1,木块与地面的最大静摩擦力等于滑动摩擦力.现有一质量为M=2.5kg的小铅块(视为质点),以v0=4m/s的初速度向右滑上左边第一木块的左端,它与木块的动摩擦因数μ2=0.2.小铅块刚滑到第四块木块时,木块开始运动,求: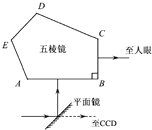 图为单反照相机取景器的示意图,ABCDE为五棱镜的一个截面,AB⊥BC.光线垂直AB 射入,分别在CD 和EA 上发生反射,且两次反射的入射角相等,最后光线垂直BC 射出.若两次反射都为全反射,则该五棱镜折射率的最小值是多少?(计算结果可用三角函数表示)
图为单反照相机取景器的示意图,ABCDE为五棱镜的一个截面,AB⊥BC.光线垂直AB 射入,分别在CD 和EA 上发生反射,且两次反射的入射角相等,最后光线垂直BC 射出.若两次反射都为全反射,则该五棱镜折射率的最小值是多少?(计算结果可用三角函数表示)