题目内容
5.甲乙两个物体都做匀加速直线运动,从同一时刻开始计时的一段时间内,两物体的位移相等,则在这段时间内( )| A. | 甲的初速度一定等于乙的初速度 | |
| B. | 甲的平均速度一定等于乙的平均速度 | |
| C. | 甲的速度变化量一定等于乙的速度变化量 | |
| D. | 甲的速度变化一定和乙的速度变化一样快 |
分析 要正确解答本题必须熟练掌握匀变速直线运动公式:x=${v}_{0}t+\frac{1}{2}a{t}^{2}$,△v=a△t,x=v0+at.并且抓住关键条件:相同时间,据此可正确解答本题.
解答 解:A、匀变速直线运动位移公式:x=${v}_{0}t+\frac{1}{2}a{t}^{2}$,已知两物体在相等的时间内的位移相等,由于不知道物体的加速度,所以不能判断出甲、乙两个物体的初速度的关系.故A错误;
B、根据平均速度v=$\frac{x}{t}$得两物体在相等的时间内的位移相等,甲、乙两物体平均速度相等,故B正确.
C、根据△v=a△t,由于不知道物体的加速度,所以不能判断出甲的速度变化量与乙的速度变化量的关系,故C错误.
D、由于不知道甲、乙两物体的初速度大小关系,根据x=${v}_{0}t+\frac{1}{2}a{t}^{2}$,得无法比较二者加速度的大小关系,不能判断出甲的速度变化是否和乙的速度变化一样快,故D错误.
故选:B.
点评 对于运动学公式要全面理解,要明确公式中各个物理量的含义、公式适用条件等,不可片面的从某一角度理解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.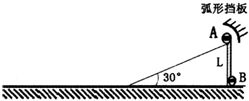 如图所示,倾角30°、高为L的固定斜面底端与光滑水平面平滑相连,质量分别为3m、m的两个小球A、B用一根长为L的轻绳连接,A球置于斜面顶端.现由静止释放A、B两球,B球与弧形挡板碰撞过程时间极短无机械能损失,且碰后只能沿斜面下滑,两球最终均滑到水平面上.已知重力加速度为g,不计一切摩擦,则( )
如图所示,倾角30°、高为L的固定斜面底端与光滑水平面平滑相连,质量分别为3m、m的两个小球A、B用一根长为L的轻绳连接,A球置于斜面顶端.现由静止释放A、B两球,B球与弧形挡板碰撞过程时间极短无机械能损失,且碰后只能沿斜面下滑,两球最终均滑到水平面上.已知重力加速度为g,不计一切摩擦,则( )
 如图所示,倾角30°、高为L的固定斜面底端与光滑水平面平滑相连,质量分别为3m、m的两个小球A、B用一根长为L的轻绳连接,A球置于斜面顶端.现由静止释放A、B两球,B球与弧形挡板碰撞过程时间极短无机械能损失,且碰后只能沿斜面下滑,两球最终均滑到水平面上.已知重力加速度为g,不计一切摩擦,则( )
如图所示,倾角30°、高为L的固定斜面底端与光滑水平面平滑相连,质量分别为3m、m的两个小球A、B用一根长为L的轻绳连接,A球置于斜面顶端.现由静止释放A、B两球,B球与弧形挡板碰撞过程时间极短无机械能损失,且碰后只能沿斜面下滑,两球最终均滑到水平面上.已知重力加速度为g,不计一切摩擦,则( )| A. | A球刚滑至水平面时的速度大小为$\frac{{\sqrt{5gL}}}{2}$ | |
| B. | B球刚滑至水平面时的速度大小为$\frac{{\sqrt{6gL}}}{2}$ | |
| C. | 在A球沿斜面下滑的过程中,轻绳对B球先做正功、后不做功 | |
| D. | 两小球在水平面上不可能相撞 |
16.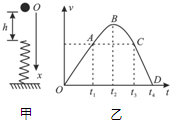 蹦床运动可简化为一个落到竖直放置的轻弹簧的小球运动,如图甲所示.质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.以小球刚下落开始计时,以竖直向下为正方向,小球的速度v随时间t变化的图线如图乙所示.图线中的OA段为直线,与曲线ABCD相切于A点.不考虑空气阻力,则关于小球的运动过程,下列说法正确的是( )
蹦床运动可简化为一个落到竖直放置的轻弹簧的小球运动,如图甲所示.质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.以小球刚下落开始计时,以竖直向下为正方向,小球的速度v随时间t变化的图线如图乙所示.图线中的OA段为直线,与曲线ABCD相切于A点.不考虑空气阻力,则关于小球的运动过程,下列说法正确的是( )
 蹦床运动可简化为一个落到竖直放置的轻弹簧的小球运动,如图甲所示.质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.以小球刚下落开始计时,以竖直向下为正方向,小球的速度v随时间t变化的图线如图乙所示.图线中的OA段为直线,与曲线ABCD相切于A点.不考虑空气阻力,则关于小球的运动过程,下列说法正确的是( )
蹦床运动可简化为一个落到竖直放置的轻弹簧的小球运动,如图甲所示.质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.以小球刚下落开始计时,以竖直向下为正方向,小球的速度v随时间t变化的图线如图乙所示.图线中的OA段为直线,与曲线ABCD相切于A点.不考虑空气阻力,则关于小球的运动过程,下列说法正确的是( )| A. | t2-t1>t3-t2 | |
| B. | 下落h高度时小球速度最大 | |
| C. | 小球在t4时刻所受弹簧弹力大于2mg | |
| D. | 小球在t2时刻重力势能和弹簧的弹性势能之和最大 |
13.用铁锤将一铁钉击入木块,设木块对铁钉的阻力与铁钉进入木块内的深度成正比,在铁锤击打第一次后,能把铁钉击入木块内1cm,则击第二次后,能击入的深度为(设铁锤每次做功相等)( )
| A. | 0.01cm | B. | 0.21cm | C. | 0.41cm | D. | 0.51cm |
20.伽利略在比萨斜塔上面做的著名的两个小球同时落地的实验,以及通过斜面实验得出自由落体运动的规律,从而开创了研究自然规律的科学方法,这种科学方法不包括的是( )
| A. | 总结归纳法 | B. | 逻辑思维 | C. | 科学实验 | D. | 数学推导 |
8.在“研究平抛物体的运动”的实验中,让小球多次沿同一轨道运动,通过描点法画小球作平抛运动的轨迹.为了能较准确地描绘运动轨迹,下面列出了一些操作要求,你认为正确的是( )
| A. | 斜槽必须光滑 | |
| B. | 通过调节使斜槽的末端保持水平 | |
| C. | 每次释放小球的位置必须相同 | |
| D. | 每次必须由静止释放小球 | |
| E. | 记录小球位置用的木条(或凹槽)每次必须严格的等距离下降 | |
| F. | 小球运动时不应与木板上的白纸(或方格纸)相接触 | |
| G. | 将球的位置记录在纸上后,取下纸,用直尺将点连成折线 |
5.假如一颗做匀速圆周运动的人造地球卫星的轨道半径增大到原来的2倍,仍做匀速圆周运动,则( )
| A. | 根据公式v=ωr,可知卫星运动的线速度将增大到原来的2倍 | |
| B. | 根据公式F=m$\frac{{v}^{2}}{r}$可知卫星所需的向心力将减少到原来的$\frac{1}{2}$ | |
| C. | 根据公式F=G$\frac{Mm}{{r}^{2}}$可知地球提供的向心力将增加到原来的$\frac{1}{4}$ | |
| D. | 根据上述(B)和(C)给出的公式,可知卫星运动的线速度将减少到原来的$\frac{\sqrt{2}}{2}$ |