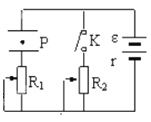
题目内容
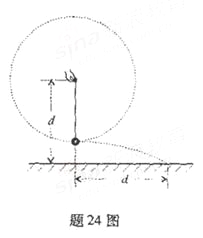
【题目】晓明站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质量为m的小球，甩动手腕，使球在竖直平面内做圆周运动，当球某次运动到最低点时，绳突然断掉。球飞离水平距离d后落地，如题24图所示，已知握绳的手离地面高度为d，手与球之间的绳长为
，重力加速度为g忽略手的运动半径和空气阻力。
（1） 求绳断时球的速度大小v1，和球落地时的速度大小v2
（2） 问绳能承受的最大拉力多大？
（3） 改变绳长，使球重复上述运动。若绳仍在球运动到最低点时断掉，要使球抛出的水平距离最大，绳长应为多少？最大水平距离为多少？
【答案】解：
（1）v1=
v2=
(2)T=
mg
(3) 当l＝
时，x有极大值xmax＝
d
【解析】
试题
(1)设绳断后球飞行时间为t，由平抛运动规律，有：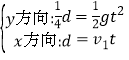
，所以
。根据机械能守恒定律则：
，所以
(2)设绳能承受的最大拉力大小为F，这也是球受到绳的最大拉力大小．球做圆周运动的半径为
，根据圆周运动向心力公式
，解得
。
(3)设绳长为l，绳断时球的速度大小为v3，绳承受的最大拉力不变，有
得
绳断后球做平抛运动，竖直位移为
,水平位移为x，时间为
，有
得
，根据一元二次方程的特点，当
时，x有极大值，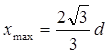
练习册系列答案
相关题目
