题目内容
13. 如图所示,一位杂技演员骑摩托车沿竖直面内的一个固定圆轨道做特技表演.他控制车的速度始终保持在20m/s,人与车的总质量为100kg,轨道对车的阻力大小是轨道对车压力的0.1倍,已知车通过最低点A时发动机的即时功率为9kW,求车通过最高点B时发动机的瞬时功率.
如图所示,一位杂技演员骑摩托车沿竖直面内的一个固定圆轨道做特技表演.他控制车的速度始终保持在20m/s,人与车的总质量为100kg,轨道对车的阻力大小是轨道对车压力的0.1倍,已知车通过最低点A时发动机的即时功率为9kW,求车通过最高点B时发动机的瞬时功率.
分析 在最高点和最低点,结合径向的合力提供向心力,根据牛顿第二定律求出圆轨道对车的作用力,根据切向合力为零,知F=f=0.1FN,根据P=Fv求解功率.
解答 解:在最低点A,根据牛顿第二定律得:
FN-mg=m$\frac{{v}^{2}}{R}$…①
PA=0.1FNv…②
在最高点,根据牛顿第二定律得:FNB+mg=m$\frac{{v}^{2}}{R}$…③
PB=Fv=0.1FNBv…④
由①②③④解得:PB=5KW
答:车通过最高点B时发动机的瞬时功率为5KW.
点评 解决本题的关键知道F=f=0.1FN,找到圆周运动向心力的来源,结合牛顿第二定律进行求解,同时解题时注意整体代换的应用,中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.夏天,如果自行车内胎充气过足,在阳光下爆晒很容易“爆胎”.“爆胎”前内胎容积视为不变,则下列说法中正确的是( )
| A. | “爆胎”前随着温度升高,车胎内气体压强将增大 | |
| B. | “爆胎”前随着温度升高,车胎内气体将向外放出热量 | |
| C. | “爆胎”是车胎所有气体分子的动能都急剧增大造成的 | |
| D. | “爆胎”是车胎内气体分子间斥力急剧增大造成的 |
8.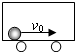 如图所示,车厢长度为L,质量为M,静止于光滑的水平面上,车厢内有一质量为m的物体以初速度v0向右运动,与车厢撞n次后静止于车厢中,这时车厢的速度为( )
如图所示,车厢长度为L,质量为M,静止于光滑的水平面上,车厢内有一质量为m的物体以初速度v0向右运动,与车厢撞n次后静止于车厢中,这时车厢的速度为( )
 如图所示,车厢长度为L,质量为M,静止于光滑的水平面上,车厢内有一质量为m的物体以初速度v0向右运动,与车厢撞n次后静止于车厢中,这时车厢的速度为( )
如图所示,车厢长度为L,质量为M,静止于光滑的水平面上,车厢内有一质量为m的物体以初速度v0向右运动,与车厢撞n次后静止于车厢中,这时车厢的速度为( )| A. | 0 | B. | v0 | C. | $\frac{m{v}_{0}}{M+m}$ | D. | $\frac{M{v}_{0}}{M-m}$ |
3.设月球绕地球转动的轨迹为圆,半径为R1、周期为27天,地球同步卫星的轨道半径为R2,则R1:R2=( )
| A. | 3:1 | B. | 6:1 | C. | 9:1 | D. | 27:1 |
 如图所示,M、N为两块带等量异种电荷的平行金属板,两板间电压可取从零到某一最大值之间的各种数值.静止的带电粒子带电荷量为+q,质量为m(不计重力),从点P经电场加速后,从小孔Q进入N板右侧的匀强磁场区域,磁感应强度大小为B,方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为θ=45°,孔Q到板的下端C的距离L,当M、N两板间电压取最大值时,粒子恰垂直打在CD板上,求:
如图所示,M、N为两块带等量异种电荷的平行金属板,两板间电压可取从零到某一最大值之间的各种数值.静止的带电粒子带电荷量为+q,质量为m(不计重力),从点P经电场加速后,从小孔Q进入N板右侧的匀强磁场区域,磁感应强度大小为B,方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为θ=45°,孔Q到板的下端C的距离L,当M、N两板间电压取最大值时,粒子恰垂直打在CD板上,求: