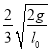题目内容

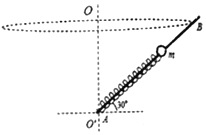
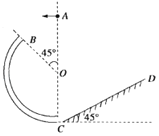
【题目】如图所示，AB为竖直平面内某圆周的竖直直径，BC与CD为两根固定光滑细直杆，其中CD通过O点且与AB成60°夹角，两细直杆上各套有一个小球，小球可视为质点。两小球均从C点由静止释放，一小球从C点运动到D点所用的时间为t1，另一小球从C点运动到B点所用的时间为t2，则t1：t2等于（　　）

A. ：1B. 2：1C. 1：1D. ：2

【答案】A

【解析】

设AB＝CD＝d。小球从C点运动到D点的过程，由牛顿第二定律有：mgsin30°＝ma1

得：a1g

由位移公式有：da1t12；得：t1＝2

小球从C点运动到B点的过程，由牛顿第二定律有：mgsin60°＝ma1

得：a2g

由位移公式有：dcos30°a2t22

得：t2

所以有：t1：t2：1

A. ：1，与结论相符，选项A正确；

B. 2：1，与结论不相符，选项B错误；

C. 1：1，与结论不相符，选项C错误；

D. ：2，与结论不相符，选项D错误；

练习册系列答案
相关题目

【题目】2018年5月和12月，我国分别成功地将探月工程的鹊桥号中继星和嫦娥四号登月探测器发射升空。鹊桥号中继星是世界首颗运行于地月拉格朗日L2点的通信卫星，为在月球背面工作的 嫦娥四号登月探测器提供地月间的中继通信。该L2点位于地球和月亮连线的延长线上，如图所示，鹊桥号在该点消耗很少燃料就可较长期地与月球同步绕地球做圆周运动。嫦娥四号登月探测器软着陆月球背面，更深层次地探测月球地质、资源等方面的信息。请根据上述信息和你所掌握的物理知识，确定下列叙述中正确的是

A. 地球对鹊桥号的万有引力作用可忽略不计

B. 以同样的速度爬上相同的坡道，探测器在月球上将比在地球上消耗更大的功率

C. 相对月面静止的探测器绕地球运行的向心加速度比鹊桥号的向心加速度小

D. 在降落到月面的过程中，探测器和月球系统的机械能守恒

【题目】如图所示的装置用来研究光电效应现象，当用光子能量为2.5 eV的光照射到光电管上时，电流表G的读数为0.2 mA，移动变阻器的触头c，当电压表的示数大于或等于0.7 V时，电流表示数为0，则(　　)

A. 光电管阴极的逸出功为1.8 eV

B. 开关S断开后，没有电流流过电流表G

C. 改用光子能量为1.5 eV的光照射，电流表G也有电流，但电流较小

D. 光电子的最大初动能为0.7 eV

【题目】如图，一根原长为l0的轻弹簧套在光滑直杆AB上，其下端固定在杆的A端，质量为m的小球也套在杆上且与弹簧的上端相连。球和杆一起绕经过杆A端的竖直轴OO′匀速转动，且杆与水平面间始终保持30°角。已知杆处于静止状态时弹簧的压缩量为，重力加速度为g。求：

（1）求弹簧的劲度系数k；

（2）弹簧为原长时，杆的角速度为多少；

（3）在杆的角速度由0缓慢增大到过程中，小球机械能增加了多少。

【题目】如图所示，长方形金属线框abcd放在光滑绝缘的水平面上，ab边长为lab=0.5m，bc边长为lbc=1m，质量为m=1kg，电阻为R=2Ω．线框处在垂直于桌面向上的匀强磁场中，磁场的磁感应强度大小为B=1T，ab边与磁场左边界重合。现给线框ab边施加一个水平向左的拉力使线框向左运动，ab边始终与磁场左边界平行，线框中产生的电流随线框运动的距离关系如图乙所示，求：

（1）线框的后一半出磁场所用的时间；

（2）将线框拉出磁场的过程中，线框中产生的焦耳热。

【题目】地球某卫星的工作轨道为圆轨道，轨道高度为h，运行周期为T．若还知道引力常量和地球半径，仅利用以上条件能求出的是（　　）

A. 地球表面的重力加速度

B. 地球对该卫星的吸引力

C. 该卫星绕地球运行的速度

D. 该卫星绕地球运行的加速度

【题目】一块足够长的白板，位于水平桌面上，处于静止状态．一石墨块（可视为质点）静止在白板上．石墨块与白板间有摩擦，滑动摩擦系数为μ．突然，使白板以恒定的速度v0做匀速直线运动，石墨块将在板上划下黑色痕迹．经过某段时间t，令白板突然停下，以后不再运动．在最后石墨块也不再运动时，白板上黑色痕迹的长度可能是（已知重力加速度为g，不计石墨与板摩擦划痕过程中损失的质量）（　　）

A. B. C. D. v0t

【题目】如图所示，BC为半径rm竖直放置的细圆管，O为细圆管的圆心，在圆管的末端C连接倾斜角为45°、动摩擦因数μ＝0.6的足够长粗糙斜面，一质量为m＝0.5kg的小球从O点正上方某处A点以v0水平抛出，恰好能垂直OB从B点进入细圆管，小球过C点时速度大小不变，小球冲出C点后经过s再次回到C点。（g＝10m/s2）求：

（1）小球从O点的正上方某处A点水平抛出的初速度v0为多大？

（2）小球第一次过C点时轨道对小球的支持力大小为多少？

（3）若将BC段换成光滑细圆管，其他不变，仍将小球从A点以v0水平抛出，且从小球进入圆管开始对小球施加了一竖直向上大小为5N的恒力，试判断小球在BC段的运动是否为匀速圆周运动，若是匀速圆周运动，求出小球对细管作用力大小；若不是匀速圆周运动则说明理由。

【题目】如图，两足够长的光滑平行导轨水平放置，处于磁感应强度为B、方向竖直向上的匀强磁场中，导轨间距为L，一端连接阻值为R的电阻。一金属棒垂直导轨放置，质量为m，接入电路的电阻为r。水平放置的轻弹簧左端固定，右端与金属杆中点链接，弹簧劲度系数为k。装置处于静止状态。现给导体棒一个水平向右的初速度v0，第一次运动到最右端时，棒的加速度为a，棒与导轨始终接触良好，导轨电阻不计，弹簧在弹性限度内，重力加速度为g，求：

（1）金属棒开始运动时受到的安培力F的大小和方向;

（2）金属棒从开始运动到第一次运动到最右端时，通过R的电荷量q；

（3）金属棒从开始运动到最终停止的整个过程中，R上产生的热量Q。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网