题目内容
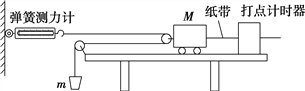
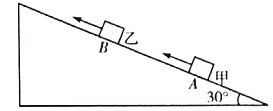
【题目】如图（甲）所示，地面上有一长为l=1m，高为h=0.8m，质量M=2kg的木板，木板的右侧放置一个质量为m=1kg的木块（可视为质点），已知木板与木块之间的动摩擦因数为μ1=0.4，木板与地面之间的动摩擦因数为μ2=0.6，初始时两者均静止。现对木板施加一水平向右的拉力F，拉力F随时间的变化如图（乙）所示，取g＝10 m/s2。求：
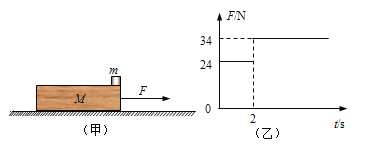
（1）前2s木板的加速度；
（2）木块落地时距离木板左侧的水平距离
。
【答案】（1）
（2）
【解析】
根据图像可以知道不同时刻受到的外力大小，再利用牛顿第二定律求解木块的加速度；根据木块和木板的受力分析各自的加速度和运动情况，利用运动学公式分析求解。
（1）因为木块在木板上滑行的最大加速度为
mg =ma1
解得：a1=4m/s2
保持木块与木板一起做匀加速运动最大拉力Fm=
(M+m)g+(M+m)a1=30N。
因F1=24N<Fm=30N，故木块与木板一起做匀加速运动，其加速度a由牛顿运动定律可得：
F－(M+m)g＝(M+m)a
解得：a=2m/s2
（2）2s末木块与木板的速度为v，由运动学知识可得：v=at1
2s后F2=34>Fm=30N，木块和木板发生相对滑动，木块加速度a1，木板加速度a2为：
F－mg－(M+m)g＝Ma2
经时间t2二者分离，此时由运动学知识可得：
vt2+
a2 t22－（vt2+a1 t22）＝l
解得：a2=6m/s2，t2=1s
此时木块的速度v块=v+ a1 t2
木板的速度：v板= v+ a2 t2
木块与木板分离至滑落到地的时间为t3，由平抛运动知识可得：
h=g t32
在木块与木板分离至滑落到地的时间为t3内，木块在水平方向向前的位移为：
S块=v块t3
木块与木板分离后，木板的加速度为a3，由牛顿运动定律可得：
F－Mg＝Ma3
在木块与木板分离至滑落到地的时间t3内，木板在水平方向向前的位移为：
S板=v板t3+a3 t32
所以，木块落地时距离木板左侧：
s= S板－S块
联立以上式子解得：s=1.68m
