��Ŀ����
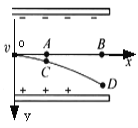
����Ŀ����ͼ����ֱ���ڵ����߹��AB����͵�B��������ˮƽ��������һλ��ͬһ��ֱ���ڡ��뾶R=0.40m�Ĺ⻬Բ�ι��ƽ�����ӣ�����һ����m=0.10kg�Ļ��飨����Ϊ�ʵ㣩����λ�ڹ���ϵ�A���ɾ�ֹ��ʼ���£����龭B���ǡ����ͨ��Բ�ι������ߵ�C����֪A�㵽B��ĸ߶�h=1.5m���������ٶ�g=10m/s2 �� ���������ɺ��Բ��ƣ���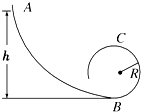
��1������ͨ��Բ�ι��B��ʱ�Թ����ѹ����С��
��2�������A�㻬��B��Ĺ����У��˷�Ħ�����������Ĺ���
���𰸡�
��1��
�⣺��ǡ��ͨ��C�㣬�Ի�����C�㣬
����ţ�ٵڶ������У�mg=m ![]() ���������ݽ�ã�vC=2m/s��
���������ݽ�ã�vC=2m/s��
���ڻ����B�㵽C��Ĺ��̣����ݻ�е���غ㶨���У�
![]() mvB2=
mvB2= ![]() mvC2+2mgR��
mvC2+2mgR��
������B��������mg�����֧����FN��
����ţ�ٵڶ�������FN��mg=m ![]() ��
��
�������ݽ�ã�FN=6mg=6N��
����ţ�ٵ������ɿ�֪��������B��ʱ�Թ����ѹ����СFN��=6N
��2��
�⣺�����A�㻬��B��Ĺ����У����ݶ��ܶ����У�
mgh��W��= ![]() mvB2��0��
mvB2��0��
�����ã�W��=0.5J
����������1��������Բ���˶���Ӧ��ţ�ٵڶ��������е���غ㶨�ɿ������֧������Ȼ�����ѹ������2����A��B����Ӧ�ö��ܶ�����������������Ĺ���

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�