��Ŀ����
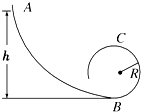
����Ŀ���ڿռ���ȡ����ϵOxy���ڵ�һ������ƽ����y�������MN��y�����Ϊd����y�ᵽMN֮����������һ����y�����������ǿ�糡���糡ǿ�ȴ�СΪE����ͼ��ʾ�����ٿɺ��Եĵ��Ӿ���һ�����Ʋ�U0δȷ���ĵ糡ֱ���ٺ�y���ϵ�A����ƽ����x��ķ��������һ��������A������Ϊ��0��h�������Ƶ��ӵ�������

��1�������Ӿ���x��ʱ������Ϊ��2d��0��������ٵ糡�ĵ��Ʋ�U0��
��2�����ٵ糡�ĵ��Ʋ�U0��ͬ�����Ӿ���x��ʱ������Ҳ��ͬ����д�����Ӿ���x��ʱ����������ٵ糡�ĵ��Ʋ�U0�Ĺ�ϵʽ����ֻҪ��д�����������д�����̣�
���𰸡���1��![]() ��2��
��2��![]() ʱ��
ʱ�� ![]()
![]() ʱ��
ʱ�� ![]()
��������������������ݶ��ܶ���������ӽ���糡ʱ���ٶȣ��ڵ糡������ƽ���˶����뿪��ǿ�糡��������ֱ���˶������뿪�糡�������ֱ���˶���Ȼ�ֽ�Ϊˮƽ�������ֱ����ץסˮƽλ�ƺ���ֱλ�ƹ�ϵ�������˶�ѧ��ʽ����������ٵ糡�ĵ��Ʋ�U0�����ٵ糡��Сʱ�����ӵ�ˮƽλ�ƿ���С��d��������������ۣ����ӳ��糡����x������Ӳ����糡����x������糡ʱ��������x�������Ϊ��ƽ���˶���ˮƽλ�ƣ����糡����x��ʱ�������ƽ���˶����糡ʱ�ķ��ٶȣ��Լ���ֱ�����ϵ�λ�ƣ�Ȼ���糡���˶��ֽ�Ϊˮƽ�������ֱ����ͨ����ʱ�������x���������
��1������ӵĵ����Ϊe������Ϊm�����Ӿ����糡���ٺ����ٶ�v0
���ݶ��ܶ����� ![]()
��������ǿ�糡���˶�����![]()
���ӵļ��ٶ�Ϊ�� ![]()
ƫתλ��Ϊ�� ![]()
�뿪�糡ʱ����ֱ�ٶ�Ϊ�� ![]()
�뿪�糡�������˶�ˮƽλ��Ϊ�� ![]()
��ֱλ��Ϊ�� ![]()
�����ϸ�ʽ��ü��ٵ糡�ĵ��Ʋ��� ![]()
��2��![]() ʱ�������糡ʱ���У�
ʱ�������糡ʱ���У� ![]()
![]() ʱ�����糡����x��ʱ���У�
ʱ�����糡����x��ʱ���У� ![]()