��Ŀ����
����Ŀ����ͼ��ʾ���뾶ΪR�İ����������̶���ˮƽת̨�ϣ�ת̨�ƹ���������O����ֱ�����Խ��ٶ�������ת����������ͬ��С���A��B������ת����������ھ�ֹ��A��B������O����������ֱ����ļнǷֱ�Ϊ��������������.����
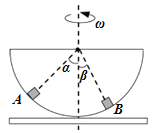
A. A������һ��С��B������
B. A��B�ܵ���Ħ��������ͬʱΪ��
C. ��A����Ħ��������B�������������ϵ�Ħ����
D. ��������A��B�ܵ���Ħ�������ܶ�����
���𰸡�D
��������
A����ܵ���Ħ����ǡ��Ϊ�㣬��������֧�����ĺ����ṩ������������ţ�ٵڶ����ɣ���Ͻ��ٶȵĴ�С������ʽ��������ʱB����Ħ�����ķ���������֧�����ĺ��������ṩ��������Ħ���������عޱ��������£�����ţ�ٵڶ��������Ħ�����Ĵ�С��
��BĦ����ǡΪ��ʱ������������ͼ
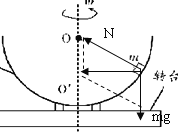
����ţ�ٵڶ����ɵã�![]()
��ã�![]()
ͬ���ɵã�![]()
���ת�����ٶ������������أ��������ж������Ĵ�С
����![]() ������
������![]() ����A��B�ܵ���Ħ����������ͬʱΪ�㣻
����A��B�ܵ���Ħ����������ͬʱΪ�㣻
��A����Ħ��������ʱת̨�Ľ��ٶ�Ϊ![]() ������B�������������ڲ�Ħ����Ϊ��ʱ�Ľ��ٶȣ����Դ�ʱB�������������µ�Ħ������
������B�������������ڲ�Ħ����Ϊ��ʱ�Ľ��ٶȣ����Դ�ʱB�������������µ�Ħ������
���ת̨���ٶȴ�A����Ħ������ʼ����A��B�����������������ܵ�Ħ��������
��ѡ��D��