��Ŀ����
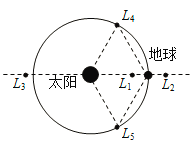
����Ŀ��1772�꣬�����������ѧ���������������ġ��������⡷ָ�����������������������壨��̫���͵�������ͬһƽ������5������㣬��ͼ�е�L1��L2��L3��L4��L5��ʾ�����dz�Ϊ�������յ㣮��������λ����Щ���ϣ�����̫�������ͬ���������£����Լ���������ȼ�϶����������ͬ����̫����Բ���˶���������һ�����Ƕ�λ����������L2�㣬����˵����ȷ���ǣ�������
A. ��������̫���˶����ں͵�����ת�������
B. ��������L2�㴦��ƽ��״̬
C. ��������̫���˶������ļ��ٶȴ��ڵ�����̫���˶������ļ��ٶ�
D. ��������L2������̫���͵��������ĺ�������L1����
���𰸡�CD
����������������������������ͬ����̫����Բ���˶���������ͬ�����ڷ�ƽ��״̬���ɵ����̫���������ĺ����ṩ�����������ݹ�ʽ![]() ���ļ��ٶȺ���������ϵ��
���ļ��ٶȺ���������ϵ��
�����������ͬ����̫����Բ���˶������������̫���˶����ں͵�����̫���˶�������ȣ����������ת����û�й�ϵ����A�����������ܵĺ���Ϊ�����̫�����������ĺ���������������������ͬ��������Ϊ�㣬���ڷ�ƽ��״̬����B�������ڸ������������̫����Բ���˶���������ͬ�������ǵĹ���뾶���ݹ�ʽ![]() ������֪�����϶����������̫���˶������ļ��ٶȴ��ڵ�����̫���˶������ļ��ٶȣ���C��ȷ�� ��Ϊ��Щ���ϵ�������ͬ������
������֪�����϶����������̫���˶������ļ��ٶȴ��ڵ�����̫���˶������ļ��ٶȣ���C��ȷ�� ��Ϊ��Щ���ϵ�������ͬ������![]() �ɵð뾶Խ�����ļ��ٶ�Խ�����Ը���
�ɵð뾶Խ�����ļ��ٶ�Խ�����Ը���![]() �ɵð뾶Խ���ܵ��ĺ���Խ��D��ȷ
�ɵð뾶Խ���ܵ��ĺ���Խ��D��ȷ