��Ŀ����
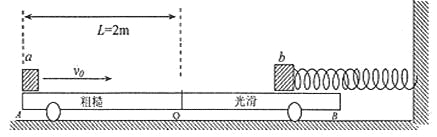
����Ŀ����ͼ��ʾ���̶��Ĺ⻬����������Ϊ![]() ��������費�����϶�
��������費�����϶�![]() �������ֵΪ
�������ֵΪ![]() �ĵ���������ƽ����ˮƽ��ļн�Ϊ
�ĵ���������ƽ����ˮƽ��ļн�Ϊ![]() ���Ҵ��ڴŸ�Ӧǿ�ȴ�СΪ
���Ҵ��ڴŸ�Ӧǿ�ȴ�СΪ![]() ����ֱ�ڵ���ƽ�����ϵ���ǿ�ų��С�����Ϊ
����ֱ�ڵ���ƽ�����ϵ���ǿ�ų��С�����Ϊ![]() ������Ϊ
������Ϊ![]() �ĵ������̶�������������ڵ����ϡ���ʼʱ��������ǡ������Ȼ����������������ع�����ϵij��ٶ�
�ĵ������̶�������������ڵ����ϡ���ʼʱ��������ǡ������Ȼ����������������ع�����ϵij��ٶ�![]() �������˶������е����ʼ���뵼�촹ֱ���������ýӴ�����֪���ɵľ���ϵ��Ϊ
�������˶������е����ʼ���뵼�촹ֱ���������ýӴ�����֪���ɵľ���ϵ��Ϊ![]() �����ɵ����������뵼��ƽ�С�
�����ɵ����������뵼��ƽ�С�

(1)���ʼʱ��ͨ������![]() �ĵ���
�ĵ���![]() �Ĵ�С�ͷ���;
�Ĵ�С�ͷ���;
(2)���������һ�λص���ʼλ��ʱ���ٶȱ�Ϊ![]() �����ʱ������ļ��ٶȴ�С
�����ʱ������ļ��ٶȴ�С![]() ;
;
(3)��������վ�ֹʱ���ɵĵ�������Ϊ![]() ��������ӿ�ʼ�˶�ֱ��ֹͣ�Ĺ���������·�����Ľ�����Q��
��������ӿ�ʼ�˶�ֱ��ֹͣ�Ĺ���������·�����Ľ�����Q��
���𰸡���1��![]() ����������Ϊb��a ��2��
����������Ϊb��a ��2��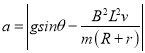 ��3��
��3��
�������������������1���������ĸ�Ӧ�綯��E1=BLv0
ͨ��R�ĵ�����С![]()
�������ֶ����жϵ�֪����������Ϊb��a
��2���������ĸ�Ӧ�綯��ΪE2=BLv
��Ӧ����![]()
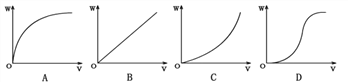
���ܵ��İ�������С![]() ��������б�����ϣ���ͼ��ʾ��
��������б�����ϣ���ͼ��ʾ��

����ţ�ٵڶ����� ��|mgsin��-F|=ma
���
��3����������վ�ֹ���� mgsin��=kx
���ɵ�ѹ����![]()
���������̻�·�����Ľ�����ΪQ0�����������غ㶨�� ��![]()
���![]()
����R�ϲ����Ľ�����

 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�