题目内容
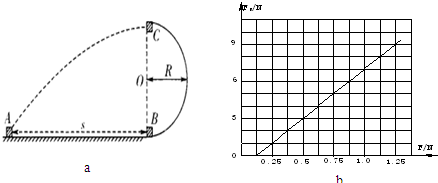
如图所示,AB段是长s=10m的粗糙水平轨道,BC段是半径R=2.5m的光滑半圆弧轨道.有一个质量m=0.1kg的小滑块,静止在A点,受一水平恒力F作用,从A点开始向B点运动,刚好到达B点时撤去力F,小滑块经半圆弧轨道从C点水平抛出,恰好落在A点,已知滑块与水平轨道间的动摩擦因数μ=0.25,g取10m/s2,
(1)求小滑块在C点的速度大小;
(2)如果要使小滑块恰好能够经过C点,求水平恒力F的大小;
(3)设小滑块经过半圆弧轨道B点时,轨道对小滑块支持力的大小为FN,若改变水平恒力F的大小,FN会随之变化.如最大静摩擦与滑动摩擦大小相等,试通过计算在坐标纸上作出FN-F图象.

(1)求小滑块在C点的速度大小;
(2)如果要使小滑块恰好能够经过C点,求水平恒力F的大小;
(3)设小滑块经过半圆弧轨道B点时,轨道对小滑块支持力的大小为FN,若改变水平恒力F的大小,FN会随之变化.如最大静摩擦与滑动摩擦大小相等,试通过计算在坐标纸上作出FN-F图象.
分析:(1)小滑块离开C点做平抛运动,根据高度求出时间,根据水平位移求出平抛运动的初速度,即小滑块在C点的速度.
(2)若小滑块恰能经过C点,根据牛顿第二定律求出C点的临界速度,再对全过程运用动能定理,求出水平恒力F的大小.
(3)根据动能定理求出由A运动到B点的速度,根据牛顿第二定律,竖直方向上合力提供向心力,求出支持力的大小,得出支持力和恒力F的关系,从而作出FN-F图象.
(2)若小滑块恰能经过C点,根据牛顿第二定律求出C点的临界速度,再对全过程运用动能定理,求出水平恒力F的大小.
(3)根据动能定理求出由A运动到B点的速度,根据牛顿第二定律,竖直方向上合力提供向心力,求出支持力的大小,得出支持力和恒力F的关系,从而作出FN-F图象.
解答:解:(1)根据2R=
gt2得,t=
=
s=1s.
则vc=
=
m/s=10m/s.
故小滑块在C点的速度大小为10m/s.
(2)小滑块恰好通过最高点有:mg=m
.
得:vc=
=5m/s.
对A到C运用动能定理得,
Fs-μmgs-mg?2R=
mvc2-0
解得:F=0.875N.
故水平恒力F的大小为0.875N.
(3)对A到B运用动能定理得,Fs-μmgs=
mvB2
在B点,根据牛顿第二定律得,FN-mg=m
联立两式解得:FN=8F-1
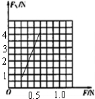
支持力最小等于重力,即FN最小为1N,所以拉力F最小为0.25N,即F≥0.25N.如图.
| 1 |
| 2 |
|
|
则vc=
| s |
| t |
| 10 |
| 1 |
故小滑块在C点的速度大小为10m/s.
(2)小滑块恰好通过最高点有:mg=m
| vc2 |
| R |
得:vc=
| gR |
对A到C运用动能定理得,
Fs-μmgs-mg?2R=
| 1 |
| 2 |
解得:F=0.875N.
故水平恒力F的大小为0.875N.
(3)对A到B运用动能定理得,Fs-μmgs=
| 1 |
| 2 |
在B点,根据牛顿第二定律得,FN-mg=m
| vB2 |
| R |
联立两式解得:FN=8F-1
支持力最小等于重力,即FN最小为1N,所以拉力F最小为0.25N,即F≥0.25N.如图.

点评:本题综合运用了牛顿第二定律和动能定理,运用动能定理解题时要合适地选择研究的过程,根据动能定理列出表达式求解.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 (2013?德州二模)如图所示,AB段为一半径R=0.2m的光滑
(2013?德州二模)如图所示,AB段为一半径R=0.2m的光滑