题目内容
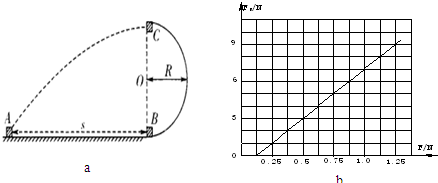
如图(a)所示,AB段是长S=10m的粗糙水平轨道,BC段是半径R=2.5m的光滑半圆弧轨道.有一个质量m=0.1kg的小滑块,静止在A点,受一水平恒力F作用,从A点开始向B点运动,刚好到达B点时撤去力F.小滑块经过半圆弧轨道B点时,用DIS力传感器测得轨道对小滑块支持力的大小为FN,若改变水平恒力F的大小,FN会随之变化,实验得到FN-F图象如图(b),g取10m/s2.
(1)若小滑块经半圆弧轨道从C点水平抛出,恰好落在A点,则小滑块在C点的速度大小;
(2)滑块与水平轨道间的动摩擦因数为多大?
(3)要使小滑块始终不脱离轨道,求水平恒力F的范围;
(1)若小滑块经半圆弧轨道从C点水平抛出,恰好落在A点,则小滑块在C点的速度大小;
(2)滑块与水平轨道间的动摩擦因数为多大?
(3)要使小滑块始终不脱离轨道,求水平恒力F的范围;

分析:(1)小物块离开C点做平抛运动,根据高度求出平抛运动的时间,结合水平位移求出C点的速度.
(2)根据动能定理,结合牛顿第二定律抓住竖直方向上的合力提供向心力求出支持力与F的关系式,通过图象,当F=0.5N,FN=3N求出动摩擦因数.
(3)要使小滑块始终不脱离轨道,一种情况是当小球运动到与O点等高时速度恰好为零,另一种情况是恰好到最高点由重力提供向心力.结合动能定理和牛顿第二定律求出F的范围.
(2)根据动能定理,结合牛顿第二定律抓住竖直方向上的合力提供向心力求出支持力与F的关系式,通过图象,当F=0.5N,FN=3N求出动摩擦因数.
(3)要使小滑块始终不脱离轨道,一种情况是当小球运动到与O点等高时速度恰好为零,另一种情况是恰好到最高点由重力提供向心力.结合动能定理和牛顿第二定律求出F的范围.
解答:解:(1)小滑块作平抛运动,设C点的速度为vC则 s=vct (1)
2R=
gt2 (2)
由(1)、(2)式得vc=
=10m/s
(2)A到B过程,由动能定理
Fs-μmgs=
mv2 (3)
在B点,FN-mg=m
(4)
由(3)、(4)得FN=
F+(mg-
mg) (5)
由图象得,当F=0.5N,FN=3N代入(5)式得μ=0.25.
(3)要使小滑块始终不脱离轨道,则当小球运动到与O点等高时速度恰好为0,或恰好到最高点由重力提供向心力.
①当小球运动到与O点等高时速度恰好为零,
Fs-μmgs-mgR=0 (6)
同时要求小滑块能运动到B点Fs-μmgs=
mv2>0(7)
由(6)、(7)式得025N<F≤0.5N 小滑块始终不脱离轨道
②当恰好到最高点由重力提供向心力.
mg=m
(8)
Fs-μmgs-mg×2R=
mv2 (9)
由(8)、(9)式得F=0.875N,故当F≥0.875N时小滑块始终不脱离轨道.
答:(1)小滑块在C点的速度大小为10m/s.
(2)滑块与水平轨道间的动摩擦因数为0.25.
(3)水平恒力F的范围为F≥0.875N或025N<F≤0.5N.
2R=
| 1 |
| 2 |
由(1)、(2)式得vc=
| s |
| 2 |
|
(2)A到B过程,由动能定理
Fs-μmgs=
| 1 |
| 2 |
在B点,FN-mg=m
| v2 |
| R |
由(3)、(4)得FN=
| 2s |
| R |
| 2sμ |
| R |
由图象得,当F=0.5N,FN=3N代入(5)式得μ=0.25.
(3)要使小滑块始终不脱离轨道,则当小球运动到与O点等高时速度恰好为0,或恰好到最高点由重力提供向心力.
①当小球运动到与O点等高时速度恰好为零,
Fs-μmgs-mgR=0 (6)
同时要求小滑块能运动到B点Fs-μmgs=
| 1 |
| 2 |
由(6)、(7)式得025N<F≤0.5N 小滑块始终不脱离轨道
②当恰好到最高点由重力提供向心力.
mg=m
| v2 |
| R |
Fs-μmgs-mg×2R=
| 1 |
| 2 |
由(8)、(9)式得F=0.875N,故当F≥0.875N时小滑块始终不脱离轨道.
答:(1)小滑块在C点的速度大小为10m/s.
(2)滑块与水平轨道间的动摩擦因数为0.25.
(3)水平恒力F的范围为F≥0.875N或025N<F≤0.5N.
点评:本题综合考查了动能定理和牛顿第二定律,关键是理清物块的运动过程,抓住临界情况,选择合适的规律进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
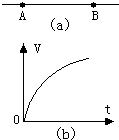 如图(a)所示,AB是某电场中的一条电场线,若在A点放置一初速度为零的电子.电子仅在电场力的作用下,沿AB由A运动到B的过程中的速度图象如图(b)所示,则下列关于A、B两点电势φ和电场强度E的判断中正确的是:( )
如图(a)所示,AB是某电场中的一条电场线,若在A点放置一初速度为零的电子.电子仅在电场力的作用下,沿AB由A运动到B的过程中的速度图象如图(b)所示,则下列关于A、B两点电势φ和电场强度E的判断中正确的是:( )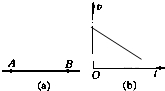 如图(a)所示,AB是某电场中的一条电场线.若有一质子以某一初速度仅在电场力的作用下,沿AB由点A运动到点B,其速度图象如图(b)所示.下列关于A、B两点的电势?和电场强度E大小的判断正确的是( )
如图(a)所示,AB是某电场中的一条电场线.若有一质子以某一初速度仅在电场力的作用下,沿AB由点A运动到点B,其速度图象如图(b)所示.下列关于A、B两点的电势?和电场强度E大小的判断正确的是( )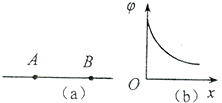 (2010?长春一模)如图(a)所示,AB是某电场中的一条电场线,若有一电子以某一初速度且仅在电场力的作用下,沿AB由点A运动到点B,所经位置的电势随距A点的距离变化的规律如图(b)所示.以下说法正确的是( )
(2010?长春一模)如图(a)所示,AB是某电场中的一条电场线,若有一电子以某一初速度且仅在电场力的作用下,沿AB由点A运动到点B,所经位置的电势随距A点的距离变化的规律如图(b)所示.以下说法正确的是( )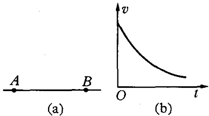 如图(a)所示,AB是某电场中的一条电场线.若有一电子以某一初速度并且仅在电场力的作用下,沿AB由点A运动到点B,其速度图象如图(b)所示.下列关于A、B两点的电势?和电场强度E大小的判断正确的是( )
如图(a)所示,AB是某电场中的一条电场线.若有一电子以某一初速度并且仅在电场力的作用下,沿AB由点A运动到点B,其速度图象如图(b)所示.下列关于A、B两点的电势?和电场强度E大小的判断正确的是( )