题目内容
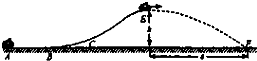 运动员驾驶摩托车做腾跃表演.如图所示,AB是平直路面,BCE为上坡路,其中BC段可视为半径R=20m的圆弧其与AB、CE平滑连接,运动员驾驶摩托车在AB段加速,到B点时速度v0=20m/s,再经过t=2s的时间通过坡面到达E点后水平飞出.已知人和车的总质量m=200kg,坡顶高度h=5m,落地点F与E点的水平距离s=16m.若摩托车的功率始终为P=15kW.
运动员驾驶摩托车做腾跃表演.如图所示,AB是平直路面,BCE为上坡路,其中BC段可视为半径R=20m的圆弧其与AB、CE平滑连接,运动员驾驶摩托车在AB段加速,到B点时速度v0=20m/s,再经过t=2s的时间通过坡面到达E点后水平飞出.已知人和车的总质量m=200kg,坡顶高度h=5m,落地点F与E点的水平距离s=16m.若摩托车的功率始终为P=15kW.求:(1)人和车从E点飞出时的速度大小?
(2)人和车过B点进入圆轨道时受到的支持力的大小?
(3)人和车从B到E的过程中重力所做的功和阻力所做的功?
分析:(1)平抛运动在水平方向做匀速直线运动,在竖直方向做自由落体运动,根据平抛运动的规律求出人和车从E点飞出的速度大小.
(2)在B点,支持力和重力的合力提供向心力,根据牛顿第二定律求出支持力的大小.
(3)根据上升的高度求出重力做功的大小,根据动能定理求出阻力做功的大小.
(2)在B点,支持力和重力的合力提供向心力,根据牛顿第二定律求出支持力的大小.
(3)根据上升的高度求出重力做功的大小,根据动能定理求出阻力做功的大小.
解答:解:(1)设摩托车在E点的速度为vE.
由s=vEt
h=
gt2
代入数据解得vE=16m/s.
(2)在B点,根据牛顿第二定律得,FN-mg=m
代入数据解得FN=6.0×103N.
(3)设摩托车在B到E的过程中,重力做功和阻力做功分别为WG、Wf,在此过程中,
WG=-mgh=-1.0×104J.
对B到E的过程运用动能定理得,
Pt+Wf+WG=
mvE2-
mvB2
代入数据解得Wf=-3.44×104J.
答:(1)人和车从E点飞出时的速度大小为16m/s.(2)人和车过B点进入圆轨道时受到的支持力的大小为6.0×103N.(3)人和车从B到E的过程中重力所做的功为-1.0×104J,阻力做功为-3.44×104J.
由s=vEt
h=
| 1 |
| 2 |
代入数据解得vE=16m/s.
(2)在B点,根据牛顿第二定律得,FN-mg=m
| vB2 |
| R |
代入数据解得FN=6.0×103N.
(3)设摩托车在B到E的过程中,重力做功和阻力做功分别为WG、Wf,在此过程中,
WG=-mgh=-1.0×104J.
对B到E的过程运用动能定理得,
Pt+Wf+WG=
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得Wf=-3.44×104J.
答:(1)人和车从E点飞出时的速度大小为16m/s.(2)人和车过B点进入圆轨道时受到的支持力的大小为6.0×103N.(3)人和车从B到E的过程中重力所做的功为-1.0×104J,阻力做功为-3.44×104J.
点评:本题考查了牛顿第二定律、动能定理的基本运用,涉及到平抛运动、圆周运动的知识,综合性较强,需加强训练.

练习册系列答案
相关题目
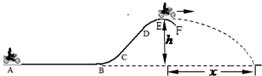 (2012?静安区一模).运动员驾驶摩托车做腾跃特技表演.如图所示,AB是水平路面,长度为L=100m,BCD是一段曲面,AB、BC相切于B点,DEF是一段半径为R=10m的圆弧曲面,E为圆弧的顶点.运动员驾驶摩托车的功率恒定.从A点由静止出发,经过t1=15s到B点,在AB段所受的阻力f=90N,摩托车过B点时速度vB=20m/s,再经t2=2s的时间,摩托车通过圆弧曲面的顶点E,此时压力传感器显示摩托车对E点的压力为零,摩托车通过E后做平抛运动,落地点与E点的水平距离为x=18m.已知人车总质量为m=180kg,重力加速度g=10m/s2.求:
(2012?静安区一模).运动员驾驶摩托车做腾跃特技表演.如图所示,AB是水平路面,长度为L=100m,BCD是一段曲面,AB、BC相切于B点,DEF是一段半径为R=10m的圆弧曲面,E为圆弧的顶点.运动员驾驶摩托车的功率恒定.从A点由静止出发,经过t1=15s到B点,在AB段所受的阻力f=90N,摩托车过B点时速度vB=20m/s,再经t2=2s的时间,摩托车通过圆弧曲面的顶点E,此时压力传感器显示摩托车对E点的压力为零,摩托车通过E后做平抛运动,落地点与E点的水平距离为x=18m.已知人车总质量为m=180kg,重力加速度g=10m/s2.求: (2004?潍坊模拟)如图所示,运动员驾驶摩托车做腾跃特技表演.运动员从斜坡底部的A处,以v0=l0m/s的初速度保持摩托车以额定功率P0=1.8kW行驶.经t=13s的时间冲上斜坡,然后从斜坡顶部已知人和车的总质量m=180kg,坡顶高度h=5m,落地点距B点的水平距离s=16m,不计空气阻力,重力加速度g=l0m/s2. 求:摩托车在冲上坡顶的过程中克服摩擦阻力做的功.
(2004?潍坊模拟)如图所示,运动员驾驶摩托车做腾跃特技表演.运动员从斜坡底部的A处,以v0=l0m/s的初速度保持摩托车以额定功率P0=1.8kW行驶.经t=13s的时间冲上斜坡,然后从斜坡顶部已知人和车的总质量m=180kg,坡顶高度h=5m,落地点距B点的水平距离s=16m,不计空气阻力,重力加速度g=l0m/s2. 求:摩托车在冲上坡顶的过程中克服摩擦阻力做的功. 运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目.如图所示,AB是水平路面,BC是半径为20m的圆弧,CDE是一段曲面.运动员驾驶功率始终为9kW的摩托车,先在AB段加速、经过4.3s到B点时达到最大速度20m/s,再经3s的时间通过坡面到达E点时关闭发动机水平飞出.已知人的质量为60kg、摩托车的质量为120kg,坡顶高度h=5m,落地点与E点的水平距离x=16m,重力加速度g=10m/s2.设摩托车在AB段所受的阻力恒定,运动员及摩托车可看作质点.求:
运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目.如图所示,AB是水平路面,BC是半径为20m的圆弧,CDE是一段曲面.运动员驾驶功率始终为9kW的摩托车,先在AB段加速、经过4.3s到B点时达到最大速度20m/s,再经3s的时间通过坡面到达E点时关闭发动机水平飞出.已知人的质量为60kg、摩托车的质量为120kg,坡顶高度h=5m,落地点与E点的水平距离x=16m,重力加速度g=10m/s2.设摩托车在AB段所受的阻力恒定,运动员及摩托车可看作质点.求: (2011?椒江区模拟)运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目.如图所示,AB是水平路面,长度为L=6m,BC是半径为R=20.75m的圆弧,AB、BC相切于B点,CDE是一段曲面.运动员驾驶功率始终为P=9kW的摩托车,从A点由静止出发,经过t1=4.3s到B点,此时压力传感器显示摩托车对地压力大小为F=3.6×104N.再经t2=3s的时间,摩托车通过坡面到达E点水平飞出.已知人的质量为m=60kg,摩托车的质量为M=120kg,运动员驾驶摩托车行驶时,前后轮着地点连线到整体重心的距离恰为r=0.75m,坡顶高度h=5m,落地点与E点的水平距离x=16m,重力加速度g=10m/s2.求:
(2011?椒江区模拟)运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目.如图所示,AB是水平路面,长度为L=6m,BC是半径为R=20.75m的圆弧,AB、BC相切于B点,CDE是一段曲面.运动员驾驶功率始终为P=9kW的摩托车,从A点由静止出发,经过t1=4.3s到B点,此时压力传感器显示摩托车对地压力大小为F=3.6×104N.再经t2=3s的时间,摩托车通过坡面到达E点水平飞出.已知人的质量为m=60kg,摩托车的质量为M=120kg,运动员驾驶摩托车行驶时,前后轮着地点连线到整体重心的距离恰为r=0.75m,坡顶高度h=5m,落地点与E点的水平距离x=16m,重力加速度g=10m/s2.求: