题目内容
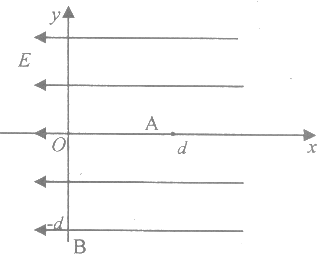
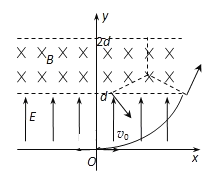
【题目】如图所示,在![]() 的一、二象限范围内分布着一个匀强电场,方向与
的一、二象限范围内分布着一个匀强电场,方向与![]() 轴正向相同,在
轴正向相同,在![]() 的一、二象限范围内分布站一个匀强磁场,方向垂直于
的一、二象限范围内分布站一个匀强磁场,方向垂直于![]() 平面向里。现将某质量为
平面向里。现将某质量为![]() 、电荷量为
、电荷量为![]() 的正粒子置于原点
的正粒子置于原点![]() ,使其以速度
,使其以速度![]() 沿
沿![]() 轴正方向射入电场。经过一段时间粒子从位置为
轴正方向射入电场。经过一段时间粒子从位置为![]() 离开电场上边缘
离开电场上边缘![]() 进入磁场,若粒子恰好没有从
进入磁场,若粒子恰好没有从![]() 的边界离开磁场。(已知
的边界离开磁场。(已知![]() ,不计粒子重力),求:
,不计粒子重力),求:

(1)电场强度![]() ;
;
(2)磁感应强度![]() ;
;
(3)粒子第一次在磁场中运动的时间。
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]()
【解析】
沿x轴正方向发射的粒子做类平抛运动,根据平抛运动基本公式列式求解E;粒子沿x轴正方向射出的粒子进入磁场偏转的角度最大,若该粒子进入磁场不能打在ab板上,则所有粒子均不能打在ab板上.根据带电粒子在电场中类平抛运动,求出进入磁场中的偏转角度,结合几何关系得出轨道半径,从而得出磁感应强度的大小;粒子运动的时间对应的圆心角,根据几何关系结合周期公式求解;
解:(1)沿x轴正方向发射的粒子有:x=1.5d,y=d
由类平抛运动基本规律得:![]() ,
,![]()
而![]()
联立可得:![]()
(2)沿x轴正方向发射的粒子射入磁场时有:![]() ,
,![]()
联立可得:![]()
![]() ,方向与水平成
,方向与水平成![]() ,斜向右上方
,斜向右上方
据题意知该粒子轨迹恰与上边缘相切,则其余粒子均达不到y=2d边界,由几何关系可知:![]()
根据牛顿第二定律得:![]()
解得:![]()
联立可得:![]()
(3)粒子运动的时间对应的圆心角,由几何关系可知圆心角为:![]()
粒子运动周期为:![]()
则时间为:![]()

练习册系列答案
相关题目