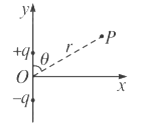Question

【题目】在科学研究中，可以通过施加适当的电场和磁场来实现对带电粒子运动的控制．如图所示的xOy平面处于匀强电场和匀强磁场中，电场强度E和磁感应强度B随时间t做周期性变化的图象如图所示．x 轴正方向为E的正方向，垂直纸面向里为B的正方向．在坐标原点O有一粒子P，其质量和电荷量分别为m和+q.不计重力．在t=时刻释放P，它恰能沿一定轨道做往复运动．

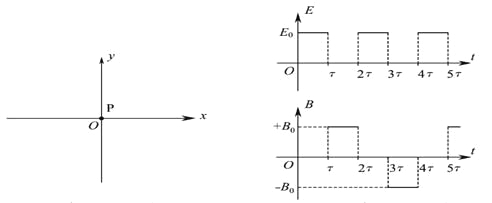
（1）求P在磁场中运动时速度的大小v0；

（2）求B0应满足的关系；

（3）在t0（0＜t0＜）时刻释放P，求P速度为零时的坐标．

Answer 1

【答案】（1）（2），（n=1，2，3……）

（3）.

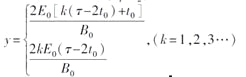【解析】

（1）对比题图可知：随着时间的变化，电场和磁场是交替产生的，有磁场前，粒子受到恒定的电场力，做匀加速直线运动．由匀变速直线运动的速度公式v=at即可求解，要注意粒子从t=才开始运动．（2）要求B0应满足的关系，首先需抓住题中的关键语：“恰能沿一定轨道做往复运动”，从而实现对本题解答的切入，然后分析粒子会做τ时间的匀速圆周运动，要想往复，则2τ时刻粒子的速度方向正好沿x轴负方向．要注意粒子做圆周运动的重复性，洛伦兹力提供向心力等．（3）从t0满足0＜t＜时刻释放，粒子将会在电场力的作用下匀加速τ-t0的时间，并以速度进入磁场，在根据对称性，找到速度为零的时刻，再根据数学的知识找到其坐标即可．

解：（1）～τ时间段内做匀加速直线运动，τ～2τ时间段内做匀速圆周运动

电场力F=qE0，加速度a=，速度v0=at，其中t=，解得v0=.

（2）只有当t=2τ时，P在磁场中做圆周运动结束并开始沿x轴负方向运动，才能沿一定轨道做往复运动，如图所示．

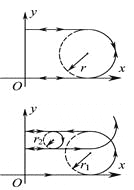
设P在磁场中做圆周运动的周期为T，则，（n=1，2，3……）

匀速圆周运动，

解得，（n=1，2，3……）

（3）在t0时刻释放，P在电场中加速时间为τ-t0，在磁场中做匀速圆周运动，

圆周运动的半径，解得

又经τ-t0时间P减速为零后向右加速时间为t0，P再进入磁场，圆周运动的半径，解得

综上分析，速度为零时横坐标x=0，相应的纵坐标为

y=或2k（r1-r2），（k=1，2，3……）

解得y=或，（k=1，2，3……）