题目内容
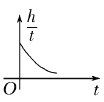
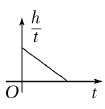
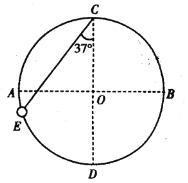
【题目】如图所示,半径为R=1m的光滑圆环竖直固定放置,AB为水平直径,CD为竖直直径。一质量为m=1kg、中间带孔的小球穿过圆环,弹性橡皮绳一端固定在圆环最高点C,另一端固定在小球上,小球静止在E点,CE与竖直方向的夹角为37°,弹性橡皮绳原长为1.5 m,弹力满足胡克定律。现沿着圆环切线向右下方给小球一个初速度v0=5 m/s。已知橡皮绳的弹性势能与橡皮绳的形变量x满足![]() ,sin37°=0.6,cos37°=0.8,g取10 m/s2,则下列说法正确的是( )
,sin37°=0.6,cos37°=0.8,g取10 m/s2,则下列说法正确的是( )
A.橡皮绳的劲度系数为k=160 N/m
B.小球运动到D点时机械能最大
C.小球运动到D点时,圆环对小球的弹力大小为70 N
D.小球能运动到C点
【答案】AD
【解析】
结合胡克定律、机械能守恒可以把答案求解出来。
A.对小球进行受力分析,由相似三角形得
![]()
![]()
![]()
解得k=160 N/m,A正确;
B.整个系统只有重力势能、弹性势能和动能相互转化,机械能守恒,B错误;
C.小球在最低点时得弹簧形变量为![]() ,设小球速度为v,由机械能守恒可得
,设小球速度为v,由机械能守恒可得
![]()
解得![]() ,所以在最低点时,弹力与重力相等,
,所以在最低点时,弹力与重力相等,
![]()
C错误;
D.由于系统得机械能守恒,所以小球能运动到C点,D正确。
故选AD。

练习册系列答案
相关题目