题目内容
在光滑水平面上有两个小木块A和B,其质量mA=1kg、mB=4kg,它们中间用一根轻质弹簧相连.一颗水平飞行的子弹质量为m=50g,以V0=500m/s的速度在极短时间内射穿两木块,已知射穿A木块后子弹的速度变为原来的
,且子弹射穿A木块损失的动能是射穿B木块损失的动能的2倍.求:系统运动过程中弹簧的最大弹性势能.
| 3 |
| 5 |

子弹穿过A时,子弹与A动量守恒,
由动量守恒定律:mv0=mAvA+mv1 ①
而由v1=
v0 得:v1=300m/s
得:vA=10m/s ②
子弹穿过B时,子弹与B动量守恒,
由动量守恒定律:mv1=mBvB+mv2 ③
又由
m
-
m
=2(
m
-
m
) ④
得:v2=100m/s
由③,④得:vB=2.5m/s ⑤
子弹穿过B以后,弹簧开始被压缩,A、B和弹簧所组成的系统动量守恒
由动量守恒定律:mAvA+mBvB=(mA+mB)v共 ⑥
由能量关系:Ep=
mA
+
mB
-
(mA+mB)
⑦
由②⑤⑥⑦得:EP=22.5J ⑧
答:系统运动过程中弹簧的最大弹性势能为22.5J.
由动量守恒定律:mv0=mAvA+mv1 ①
而由v1=
| 3 |
| 5 |
得:vA=10m/s ②
子弹穿过B时,子弹与B动量守恒,
由动量守恒定律:mv1=mBvB+mv2 ③
又由
| 1 |
| 2 |
| v | 20 |
| 1 |
| 2 |
| v | 21 |
| 1 |
| 2 |
| v | 21 |
| 1 |
| 2 |
| v | 22 |
得:v2=100m/s
由③,④得:vB=2.5m/s ⑤
子弹穿过B以后,弹簧开始被压缩,A、B和弹簧所组成的系统动量守恒
由动量守恒定律:mAvA+mBvB=(mA+mB)v共 ⑥
由能量关系:Ep=
| 1 |
| 2 |
| v | 2A |
| 1 |
| 2 |
| v | 2B |
| 1 |
| 2 |
| v | 2共 |
由②⑤⑥⑦得:EP=22.5J ⑧
答:系统运动过程中弹簧的最大弹性势能为22.5J.

练习册系列答案
相关题目
 (2007?福建模拟)如图所示,在光滑水平面上有两个物体A、B,A与轻弹簧相连并静止于水平面上,物体B沿水平方向以初速度v向右运动,跟与A相连的轻弹簧相碰.在B跟弹簧相碰后,对于A、B和轻弹簧组成的系统,下列说法中正确的是( )
(2007?福建模拟)如图所示,在光滑水平面上有两个物体A、B,A与轻弹簧相连并静止于水平面上,物体B沿水平方向以初速度v向右运动,跟与A相连的轻弹簧相碰.在B跟弹簧相碰后,对于A、B和轻弹簧组成的系统,下列说法中正确的是( ) 如图所示,在光滑水平面上有两个质量分别为m1、m2的物体,已知m1>m2,两物体间水平连接着一轻质弹簧秤,若用大小为F的水平力向右拉m1,稳定后的加速度大小为a1,弹簧秤的示数为F1;若改用大小为F的水平拉力向左拉m2,稳定后的加速度大小为a2,弹簧秤的示数为F2,则以下判断正确的是( )
如图所示,在光滑水平面上有两个质量分别为m1、m2的物体,已知m1>m2,两物体间水平连接着一轻质弹簧秤,若用大小为F的水平力向右拉m1,稳定后的加速度大小为a1,弹簧秤的示数为F1;若改用大小为F的水平拉力向左拉m2,稳定后的加速度大小为a2,弹簧秤的示数为F2,则以下判断正确的是( ) 如图所示,在光滑水平面上有两个小球A和B(可视为质点),质量mA=4kg,mB=2.0kg,球B静止在M点,球A在水平面上从很远处沿两球的中心连线以一个初速度向着B球运动.若已知在两球相距L>18m时,两球之间无相互作用力;在两球相距L≤18m时,它们之间存在着相互作用且大小恒定的斥力F.在运动过程中两球相距最近时的距离为d=6m,此时球A的瞬时速度是4m/s.求:
如图所示,在光滑水平面上有两个小球A和B(可视为质点),质量mA=4kg,mB=2.0kg,球B静止在M点,球A在水平面上从很远处沿两球的中心连线以一个初速度向着B球运动.若已知在两球相距L>18m时,两球之间无相互作用力;在两球相距L≤18m时,它们之间存在着相互作用且大小恒定的斥力F.在运动过程中两球相距最近时的距离为d=6m,此时球A的瞬时速度是4m/s.求: (2009?德阳模拟)在光滑水平面上有两个可视为质点的小球A、B,mA=1kg,mB=0.5kg在两球间存在一有限区域:当两小球均在该区域内或者任一小球在该区域内两球间就有相互作用的恒定斥力F=1N,当两小球均在该区域外时两球间无作用力.A球离作用区左边界SA=20m,B在作用区右边界处,作用区长度L=5.5m.现使A以初速度vA=8m/s、B球以初速度vB=2m/s相向运动.求:
(2009?德阳模拟)在光滑水平面上有两个可视为质点的小球A、B,mA=1kg,mB=0.5kg在两球间存在一有限区域:当两小球均在该区域内或者任一小球在该区域内两球间就有相互作用的恒定斥力F=1N,当两小球均在该区域外时两球间无作用力.A球离作用区左边界SA=20m,B在作用区右边界处,作用区长度L=5.5m.现使A以初速度vA=8m/s、B球以初速度vB=2m/s相向运动.求: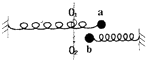 在光滑水平面上有两个完全相同的弹簧振子a和b,O1,O2为其平衡位置,如图所示.今将a向右拉伸4cm,将b向右压缩2cm,同时由静止释放,不计空气阻力.下列说法正确的是( )
在光滑水平面上有两个完全相同的弹簧振子a和b,O1,O2为其平衡位置,如图所示.今将a向右拉伸4cm,将b向右压缩2cm,同时由静止释放,不计空气阻力.下列说法正确的是( )