Question

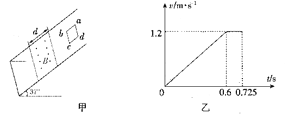
【题目】如图所示是长为8m的水平传送带AB和一竖直的半径为0.8m的形光滑轨道的组合装置轨道底端与传送带在B点相切，若传送带向右以3m/s的恒定速度匀速运动，现在圆轨道的最高点由静止释放质量为4kg的物块，物块恰好能运动到水平传送带的最左端而不掉下，重力加速度大小为g=10m/s2。求：

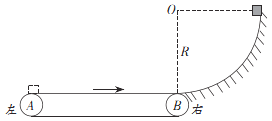
(1)物块滑到圆形轨道底端时对轨道的压力大小和物块与传送带间的动摩擦因数；

(2)物块返回到圆轨道后能够上升的高度和在传送带上第一次往返所用的时间。

Answer 1

【答案】（1）120N;0.1（2）0.45m；8.17s

【解析】

（1）利用动能定理以及向心力相关知识列出方程，同时注意求得是压力，要利用牛顿第三定律；

（2）分析物块在皮带上运动情况，然后结合机械能守恒进行求解。

（1）物块从圆形光滑轨道下滑的过程，根据机械能守恒有：

解得：

物块在光滑圆轨道最低点，根据牛顿第二定律有：

解得：

由牛顿第三定律可知，物块对轨道的压力，其中负号表示压力的方向竖直向下；

物块沿传送带滑到左端速度恰好为零，由动能定理有：

代入数据可以得到：；

（2）物块在传送带上先做匀减速运动，根据牛顿第二定律有：，则

在物块减速到零的时间为：

反向加速时加速度不变，故加速时间为：

这段时间的位移为：

之后物块随传送带匀速运动，则

物块以与传送带一样的速度滑上光滑圆轨道后，根据机械能守恒有：

代入数据可以得到：

物块在传送带上第一次往返所用的时间为：。