��Ŀ����
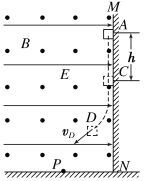
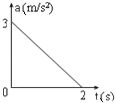
����Ŀ����ͼ��ʾ��ֱ�����ο�a�̶���ˮƽ�����ϣ����ϱ���AB������γ������=37����б��;bΪ����a������Ϊ2kg�㹻����ľ�壬�ϱ���BC��ABƽ���Խӡ�t=0ʱ������Ϊ1kg������Ϊ�ʵ�Ļ���c��A���ɾ�ֹ��ʼ�»���ͼ��c��0~ 6s�ڵ�������ʱ��t�仯��ͼ����֪c��AB��c��BC�Ķ�Ħ��������ͬ����Ϊb������Ķ�Ħ��������5������Ϊ���Ħ�������ڻ���Ħ������ȡg=10m/s2��sin37��=0.6����:

��1��c��BC�䶯Ħ������
��2��b�ڵ����ϻ�������
���𰸡���1��0.25��2��8m
��������
��1�������AB���������˶�����mgsin370-��1mgcos370=ma1
����ͼ��֪��![]()
�����1=0.25
��2����b�����֮��Ķ�Ħ������Ϊ��2�����2=0.05
��c��BC�ϻ���ʱ��c��b���ٶȵĴ�С�ֱ�Ϊa2��a3��
��1mg=ma2 ��
��1mg-��2(m+M)g=Ma3
���a2=2.5m/s2��a3=0.5m/s2
���3.0s��ʼ������ʱ��t1��c��b���ٶ����Ϊv����
v=v0-a2t1��
v=a3t1
��ã�t1=4s��v=2m/s��
ʱ��t1��ľ���λ�ƣ�x1=![]() a3t12
a3t12
���x1=4m
�Ժ�cbһ����٣����ٷ�����Ի���������ٶȵĴ�СΪa4�����2(m+M)g =(m+M)a4
���a4=0.5m/s2
�ù���b��������Ϊx2��v2=2a4x2
���x2=4m
b�����ľ���x=x1+x2
���x=8m

 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�