Question

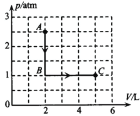
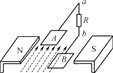
【题目】如图所示PQ、MN为足够长的两平行金属导轨，它们之间连接一个阻值R＝8Ω的电阻，导轨间距为L＝1m。一质量m＝0.1kg，电阻r＝2Ω，长约1m的金属杆水平放置在导轨上，它与导轨的滑动摩擦因数．导轨平面的倾角为θ＝30°，在垂直导轨平面方向有匀强磁场，磁感应强度B＝0.5T，现让金属杆AB由静止开始下滑，已知杆AB从静止开始到恰好作匀速运动的过程中沿轨道下滑距离s=20m，g=10m/s2求：

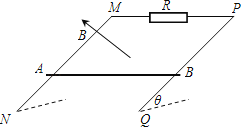
（1）杆AB下滑速度为2m/s时的加速度大小；

（2）杆AB下滑的最大速度vm；

（3）杆AB从静止开始到恰好作匀速运动的过程中R上产生的热量。

Answer 1

【答案】（1）1.5m/s2；（2）8m/s；（3）0.64J

【解析】

（1）由牛顿第二定律、安培力公式与闭合电路欧姆定律及摩擦力表达式，列出方程即可求解。

（2）当AB杆加速度减至为零时，速度达到最大，从而根据方程计算，即可求解。

（3）根据法拉第电磁感应定律、闭合电路欧姆定律、电量表达式从而列出面积与电量、电阻及磁场、杆的长度关系，再由能量守恒关系，即可求解。

（1）取AB杆为研究对象其受力分析

沿斜面方向： ①

垂直斜面方向： ②

摩擦力 ③

安培力 ④

⑤

⑥

联立上面①②③④⑤⑥解得：

当 时

（2）由上问可知 ，故AB做加速度减小的加速运动

当时，

（3）从静止开始到运速运动过程中

设两电阻发热和为QR+Qr

由能量守恒可知

又

联立 解得