题目内容
在地面上方某处的真空室里存在着水平方向的匀强电场,以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系.一质量为m、带电荷量为+q的微粒从点P(l,0)由静止释放后沿直线PQ运动.当微粒到达点Q(0,-l)的瞬间,突然将电场方向顺时针旋转90°,同时加上一个垂直于纸面向外的匀强磁场(图中未画出),磁感应强度的大小B=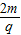
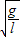 ,该磁场有理想的下边界,其他方向范围无限大.已知重力加速度为g.求:
,该磁场有理想的下边界,其他方向范围无限大.已知重力加速度为g.求:(1)匀强电场的场强E的大小
(2)欲使微粒不从磁场下边界穿出,该磁场下边界的y轴坐标值应满足什么条件?
(3)求微粒从P点开始运动到第二次经过y轴所需要的时间.

【答案】分析:(1)微粒在电场中受到电场力和重力,沿PQ方向运动,可知微粒所受的合力必定沿PQ方向,可知电场力方向水平向左,作出力的合成图,求解场强大小.
(2)电场方向顺时针旋转90°所受电场力的方向竖直向山,和重力平衡,再加上磁场后,做匀速圆周运动,临界条件是最低端速度与磁场下边界相切;
(3)微粒从P点开始运动到第二次经过y轴所需要的时间为由P到O匀加速直线运动的时间和匀速圆周运动的时间之和.
解答:解:(1)由于微粒沿PQ方向运动,可知微粒所受的合力沿PQ方向,可得
qE=mgcotα…①
由题意得α=45°…②
①②联立得: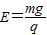
(2)电场方向顺时针旋转90°所受电场力的方向竖直向山,和重力平衡,再加上磁场后,做匀速圆周运动,运动轨迹如图所示
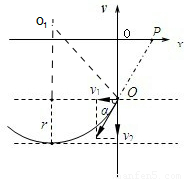
由P到Q由牛顿第二定律得:
由v2=2al得;Q点的速度为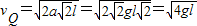 …③
…③
在磁场中洛伦兹力提供向心力得: …④
…④
③④联立得:r=l…⑤
由几何关系可得:磁场下边界距x轴的距离为;
边界越靠下越飞不出磁场,故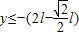
(3)粒子由P到O的时间为t1,由v=at得:
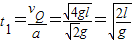 …⑥
…⑥
粒子在复合场中的匀速圆周运动如图所示:
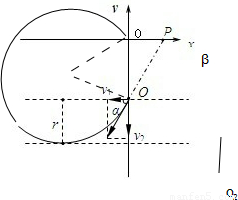
粒子的周期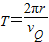 …⑦
…⑦
由几何关系可得粒子的偏转角为β=270°
则粒子在磁场中运动的时间为 …⑧
…⑧
③⑤⑧联立求解得:
微粒从P点开始运动到第二次经过y轴所需要的时间
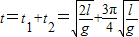
答:(1)匀强电场的场强E的大小为
(2)欲使微粒不从磁场下边界穿出,该磁场下边界的y轴坐标值应满足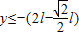
(3)求微粒从P点开始运动到第二次经过y轴所需要的时间为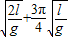
点评:本题中微粒在电场中做直线运动,抓住质点做直线运动的条件:合力与速度共线分析并求解场强的大小.加上磁场后,运用分解的方法研究洛伦兹力,此法不常用,要尝试运用.
(2)电场方向顺时针旋转90°所受电场力的方向竖直向山,和重力平衡,再加上磁场后,做匀速圆周运动,临界条件是最低端速度与磁场下边界相切;
(3)微粒从P点开始运动到第二次经过y轴所需要的时间为由P到O匀加速直线运动的时间和匀速圆周运动的时间之和.
解答:解:(1)由于微粒沿PQ方向运动,可知微粒所受的合力沿PQ方向,可得
qE=mgcotα…①
由题意得α=45°…②
①②联立得:
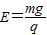
(2)电场方向顺时针旋转90°所受电场力的方向竖直向山,和重力平衡,再加上磁场后,做匀速圆周运动,运动轨迹如图所示

由P到Q由牛顿第二定律得:

由v2=2al得;Q点的速度为
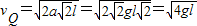 …③
…③在磁场中洛伦兹力提供向心力得:
 …④
…④③④联立得:r=l…⑤
由几何关系可得:磁场下边界距x轴的距离为;

边界越靠下越飞不出磁场,故
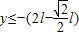
(3)粒子由P到O的时间为t1,由v=at得:
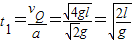 …⑥
…⑥粒子在复合场中的匀速圆周运动如图所示:

粒子的周期
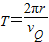 …⑦
…⑦由几何关系可得粒子的偏转角为β=270°
则粒子在磁场中运动的时间为
 …⑧
…⑧③⑤⑧联立求解得:

微粒从P点开始运动到第二次经过y轴所需要的时间
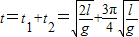
答:(1)匀强电场的场强E的大小为

(2)欲使微粒不从磁场下边界穿出,该磁场下边界的y轴坐标值应满足
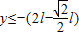
(3)求微粒从P点开始运动到第二次经过y轴所需要的时间为
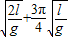
点评:本题中微粒在电场中做直线运动,抓住质点做直线运动的条件:合力与速度共线分析并求解场强的大小.加上磁场后,运用分解的方法研究洛伦兹力,此法不常用,要尝试运用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 在地面上方某处的真空室里存在着水平方向的匀强电场,以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系.一质量为m、带电荷量为+q的微粒从点P(l,0)由静止释放后沿直线PQ运动.当微粒到达点Q(0,-l)的瞬间,突然将电场方向顺时针旋转90°,同时加上一个垂直于纸面向外的匀强磁场(图中未画出),磁感应强度的大小B=
在地面上方某处的真空室里存在着水平方向的匀强电场,以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系.一质量为m、带电荷量为+q的微粒从点P(l,0)由静止释放后沿直线PQ运动.当微粒到达点Q(0,-l)的瞬间,突然将电场方向顺时针旋转90°,同时加上一个垂直于纸面向外的匀强磁场(图中未画出),磁感应强度的大小B= 在地面上方某处的真空室里存在着水平方向的匀强电场,以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系.一质量为m、带电荷量为+q的微粒从点P(
在地面上方某处的真空室里存在着水平方向的匀强电场,以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系.一质量为m、带电荷量为+q的微粒从点P(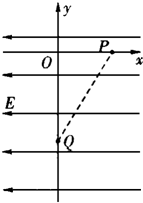 在地面上方某处的真空室里存在着水平方向的匀强电场,以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系.一质量为m、带电荷量为+q的微粒从点P(
在地面上方某处的真空室里存在着水平方向的匀强电场,以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系.一质量为m、带电荷量为+q的微粒从点P(
 ,该磁场有理想的下边界,其他方向范围无限大.已知重力加速度为g.求:
,该磁场有理想的下边界,其他方向范围无限大.已知重力加速度为g.求: 