题目内容
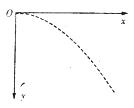
 如图是某同学在研究平抛运动实验中作出的一条平抛运动的轨迹曲线,坐标原点为抛出点.
如图是某同学在研究平抛运动实验中作出的一条平抛运动的轨迹曲线,坐标原点为抛出点.①你如何说明该曲线是一条抛物线?
②若该曲线的方程是y=
| 1 | 2 |
分析:①若该曲线是一条抛物线,则y=kx2,在轨迹上取两个点,量出坐标,若满足
=
则该曲线是一条抛物线;
②平抛运动竖直方向做自由落体运动,水平方向做匀速运动,根据平抛运动的基本公式求出y-x2的关系式,对照y=
x2即可求解.
| y1 |
| y2 |
| x12 |
| x22 |
②平抛运动竖直方向做自由落体运动,水平方向做匀速运动,根据平抛运动的基本公式求出y-x2的关系式,对照y=
| 1 |
| 2 |
解答:解:①若该曲线是一条抛物线,则y=kx2
在轨迹上取两个点,量出坐标分别为(x1,y1)、(x2,y2)
看是否满足
=
若满足则该曲线是一条抛物线.
②平抛运动竖直方向做自由落体运动,所以y=
gt2①
水平方向做匀速运动,则t=
②
由①②得:
y=
g(
)2=
x2
所以
=
解得:v0=
=3.1m/s
答:①若满足
=
则该曲线是一条抛物线;
②若该曲线的方程是y=
x2,那么平抛物体的初速度是3.1m/s.
在轨迹上取两个点,量出坐标分别为(x1,y1)、(x2,y2)
看是否满足
| y1 |
| y2 |
| x12 |
| x22 |
若满足则该曲线是一条抛物线.
②平抛运动竖直方向做自由落体运动,所以y=
| 1 |
| 2 |
水平方向做匀速运动,则t=
| x |
| v0 |
由①②得:
y=
| 1 |
| 2 |
| x |
| v0 |
| g |
| 2v02 |
所以
| g |
| 2v02 |
| 1 |
| 2 |
解得:v0=
| g |
答:①若满足
| y1 |
| y2 |
| x12 |
| x22 |
②若该曲线的方程是y=
| 1 |
| 2 |
点评:本题主要考查了平抛运动的基本公式的直接应用,知道平抛运动竖直方向做自由落体运动,水平方向做匀速运动,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图是某同学用频闪照相研究平抛运动时拍下的照片,背景方格纸的边长为10cm,A、B、C是同一小球在频闪照相中拍下的三个连续的不同位置时的照片,则:(g=10m/s2)
如图是某同学用频闪照相研究平抛运动时拍下的照片,背景方格纸的边长为10cm,A、B、C是同一小球在频闪照相中拍下的三个连续的不同位置时的照片,则:(g=10m/s2)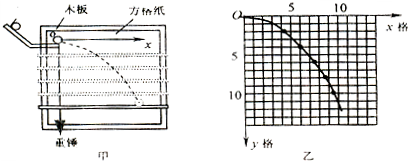
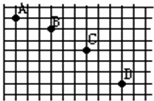 如图是某同学用频闪照相研究平抛运动时拍下的照片,背景方格纸的边长为2.5cm,A、B、C是同一小球在频闪照相中拍下的三个连续的不同位置时的照片,则:(g=10m/s2)
如图是某同学用频闪照相研究平抛运动时拍下的照片,背景方格纸的边长为2.5cm,A、B、C是同一小球在频闪照相中拍下的三个连续的不同位置时的照片,则:(g=10m/s2)