题目内容
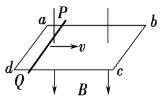
【题目】如图所示,在竖直平面内,有一长度L=2.4m的固定绝缘竖直杆AB,B点所在的水平面线上方存在着场强大小E1=5×106N/C、方向水平向右的匀强电场,下方虚线空间存在着场强大小为E2=E1、方向与竖直方向的夹角α=37°、斜向右上的匀强电场。现将一质量m=0.8kg、电荷量q=+2×10-6C的小球(可视为质点)套在杆上从A端由静止释放后下滑,最后从C点离开电场E2,此时速度方向恰好与E2垂直。已知小球与杆间的动摩擦因数μ=0.2,取g=10m/s2,sin37°=0.6,cos37°=0.8。求:
(1)小球到达B点时的速度大小vB;
(2)小球在电场E2中的加速度大小和方向,以及小球过C点时的速度vC大小;
(3)从A端释放到C点离开的过程中,电场力做的功。

【答案】(1)6m/s;(2)7.5m/s2,方向水平向右;10m/s;(3)25.6J。
【解析】
(1)小球沿杆下滑过程中受到的滑动摩擦力大小为
f=μqE1
则小球沿杆下滑的加速度大小为
![]()
由速度位移的关系式得
vB2=2aL
联立解得
vB=6m/s
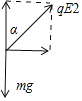
(2)小球离开B点后在匀强电场E2中的受重力、电场力,如图所示,将电场力分解
qE2cos 37°=8N
恰好与重力mg=8N平衡,小球在匀强电场E2中做类平抛运动,则加速度大小为:
![]()
解得
a=7.5m/s2
方向水平向右
小球过C点时,将速度分解,有:
![]()

(3)到C点时的水平速度
![]()
设从B到C的时间为t,则
vx=a't
解得
![]()
B、C两点间的水平距离为
![]()
电场力的功
W=qE2sin37°x=25.6J

【题目】一辆摩托车与一辆汽车在平直的公路上运动,下表是每隔1秒记录的两车的速度值。若两车的运动可看做匀变速直线运动,则下列说法正确的是( )
| 0 | 1 | 2 | 3 | 4 |
摩托车 | 18.0 | 17.5 | 17.0 | 16.5 | 16.0 |
汽车 | 9.8 | 110 | 12.2 | 13.4 | 14.6 |
A.从t=4s开始计时,经过![]() 两车的速度相等B.摩托车的速度变化快
两车的速度相等B.摩托车的速度变化快
C.在0~4s内,摩托车的平均速度较大D.摩托车的位移在减小
【题目】在《探究感应电流方向的规律》实验中
(1)用试触的方法确定电流方向与电流计指针偏转方向的关系。如图(1)所示实验表明,如果电流从负接线柱流入指针将向______偏转(填左或右)。
(2)观察如图(2)所示的线圈绕线方向,若电流从A流入到B流出,从上向下看电流的方向为______(填顺时针或逆时针)。
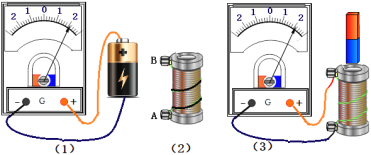
(3)用如图(3)所示的实验装置,若电流表指针向右偏转,则线圈中感应电流产生的磁场的方向_______(填向上或向下)。用电流表观察感应电流的方向,然后判断感应电流的磁场方向,得到如下实验记录。
磁铁的磁场方向 | 向下 | 向下 | 向上 | 向上 |
磁铁的磁通量的变化 | 增大 | 减小 | 增大 | 减小 |
感应电流的磁场方向 | 向上 | 向下 | 向下 | 向上 |
由些得出下列判断中正确的是_________
A.感应电流的磁场方向和磁铁的磁场方向一定相反
B.感应电流的磁场方向和磁铁的磁场方向一定相同
C.磁通量增大时,感应电流的磁场方向和磁铁的磁场方向一定相反
D.磁通量减小时,感应电流的磁场方向和磁铁的磁场方向一定相反