Question

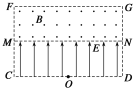
【题目】如图所示，在矩形区域CDNM内有沿纸面向上的匀强电场，场强的大小E＝1．5×105 V/m；在矩形区域MNGF内有垂直纸面向外的匀强磁场，磁感应强度大小B＝0．2 T．已知CD＝MN＝FG＝0．60 m，CM＝MF＝0．20 m．在CD边中点O处有一放射源，沿纸面向电场中各方向均匀地辐射出速率均为v0＝1．0×106 m/s的某种带正电粒子，粒子质量m＝6．4×10－27 kg，电荷量q＝3．2×10－19 C，粒子可以无阻碍地通过边界MN进入磁场，不计粒子的重力．求：

（1）粒子在磁场中做圆周运动的半径；

（2）边界FG上有粒子射出磁场的范围长度；

（3）粒子在磁场中运动的最长时间．（后两问结果保留两位有效数字）

Answer 1

【答案】（1）0．2 m （2）0．43 m （3）2．1×10－7 s

【解析】

试题分析： （1）电场中由动能定理得：

qEd＝mv2－mv

由题意知d＝0．20 m，代入数据得

v＝2×106 m/s

带电粒子在磁场中做匀速圆周运动，

qBv＝m

解得r＝＝0．2 m．

（2）设粒子沿垂直于电场方向射入时，出电场时水平位移为x，则由平抛规律得：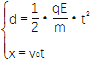

解得x＝ m

离开电场时，sin θ1＝＝，θ1＝30°．

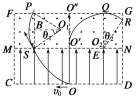
由题意可知，PS⊥MN，沿OC方向射出粒子到达P点，为左边界，垂直MN射出的粒子与边界FG相切于Q点，Q为右边界，QO″＝r，轨迹如图．

范围长度为l＝x＋r＝（＋0．2）m≈0．43 m．

（3）T＝，由分析可知，OO′方向射出的粒子运动时间最长，设FG长度为L

sin θ2＝＝，θ2＝30°

带电粒子在磁场中运动的最大圆心角为120°，对应的最长时间为tmax＝T＝≈2．1×10－7 s