题目内容
【题目】宽9m的成型玻璃以2m/s的速度连续不断地向前行进，在切割工序处，金刚割刀的速度为10m/s，为了使割下的玻璃板都成规定尺寸的矩形，则：
(1)金刚割刀的轨道应如何控制？
(2)切割一次的时间多长？
(3)所生产的玻璃板的规格是怎样的？
【答案】(1)割刀速度方向与玻璃板速度方向成arccos
角度
(2)0.92 s (3)宽9 m、长1.84 m
【解析】试题分析：为了使割下的玻璃板都成规定尺寸的矩形，知合速度的方向与玻璃板垂直，根据平行四边形定则求出金刚钻割刀的轨道方向，通过合速度求出切割一次的时间．根据等时性求出切割成的玻璃板长度．
（1）由题目条件知，割刀运动的速度是实际的速度，所以为合速度．其分速度的效果恰好相对玻璃垂直切割．
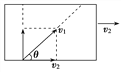
设割刀的速度v1的方向与玻璃板速度v2的方向之间的夹角为θ，如图所示。要保证割下均是矩形的玻璃板，则由v1是合速度得v2＝v1cos θ
所以cos θ＝
＝
，即θ＝arccos
所以，要割下矩形板，割刀速度方向与玻璃板速度方向所成角度为θ＝arccos
（2）切割一次的时间t＝
＝
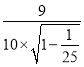s≈0．92 s
（3）切割出的矩形玻璃板的规格为：长度d＝9 m
宽度：l＝v2t＝2×0．92 m＝1．84 m
智能训练练测考系列答案
【题目】某同学利用如下图所示的装置探究功与速度变化的关系：
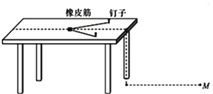
（1）小物块在橡皮筋的作用下弹出，沿水平桌面滑行，之后平抛落至水平地面上，落点即为M1；
（2）在钉子上分别套上2条、3条、4条…同样的橡皮筋，使每次橡皮筋拉伸的长度都保持一致，重复步骤（1），小物块落点分别记为M2、M3、M4…；
（3）测量相关数据，进行数据处理．
①为求出小物块从桌面抛出时的动能，需要测量下列物理量中的 （填正确答案标号，g已知）．
A．小物块的质量m |
B．橡皮筋的原长x |
C．橡皮筋的伸长量△x |
D．桌面到地面的高度h |
E．小物块抛出点到落地点的水平距离L
②将几次实验中橡皮筋对小物块做功分别记为W1、W2、W3、…，小物块抛出点到落地点的水平距离分别记为L1、L2、L3、…．若功与速度的平方成正比，则应以W为纵坐标， 为横坐标作图，才能得到一条直线．
③由于小物块与桌面之间的摩擦不能忽略，则由此引起的误差属于 （填“偶然误差”或“系统误差”）．
