Question

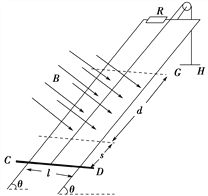
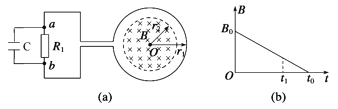
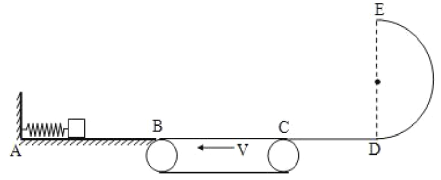
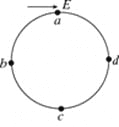
【题目】有电阻的导电圆盘半径为R，其边缘用电阻不计的导电材料包裹，可绕固定点O在水平面内转动，其轴心O和边缘处电刷A均不会在转动时产生阻力，空气阻力也忽略不计。用导线将电动势为E的电源、导电圆盘、电阻和开关连接成闭合回路，如图1所示在圆盘所在区域内充满竖直向下的匀强磁场，如图2所示只在A、O之间的一块圆形区域内存在竖直向下的匀强磁场，两图中磁场的磁感应强度大小均为B，且磁场区域固定。如果将开关S闭合，圆盘将会转动起来。

（1）在图1中，将开关S闭合足够长时间后，圆盘转速达到稳定。

a．从上往下看，圆盘的转动方向是顺时针还是逆时针？

b．求稳定时圆盘转动的角速度ω1的大小。

（2）在图2中，进行了两次操作：第一次，当圆盘加速到ω0时将开关断开，圆盘逐渐减速停下；第二次，当圆盘加速到2ω0时将开关断开，圆盘逐渐减速停下。已知从理论上可以证明：在圆盘减速过程中任意一个极短的时间△t内，角速度的变化量△ω=kF△t，F是该时刻圆盘在磁场区域受到的安培力的大小，k为常量。求两次操作中从开始减速到停下的过程中圆盘转过的角度之比θ1：θ2。

（3）由于图1中的磁场范围比图2中的大，所以刚闭合开关瞬时，图1中圆盘比图2中圆盘加速得快。有人认为：断开开关后，图1中圆盘也将比图2中圆盘减速得快。请分析说明这样的想法是否正确。

Answer 1

【答案】（1）a．从上往下看，圆盘的转动方向是逆时针。b．稳定时圆盘转动的角速度ω1的大小是。（2）θ1：θ2是1：2。（3）这样的想法错误

【解析】

（1）a．根据左手定则知：从上往下看，圆盘的转动方向是逆时针方向。

b．圆盘转动时，产生沿半径方向的感应电动势，在与轴O距离为r处沿半径方向取一小段长度△r，这一小段距离上的感应电动势为：△E感=Brω△r

从轴O到圆盘边缘处求和，可得感应电动势为：

。

当转动稳定后，圆盘的感应电动势（即反电动势）与电源电动势相等，因此有：

ω1=E

解得：ω1=。

（2）图2中开关断开圆盘减速时，由于磁场区域固定，所以仍有圆盘的感应电动势E感∝ω，且可认为圆盘中电流流经的路径及电阻不变，因此安培力F∝I∝E感∝ω，即安培力F与角速度ω成正比；

由题意知：在任意一段极短的时间△t内，角速度的变化量△ω=kF△t，考虑到其中F∝ω，可知△ω=k′ω△t（k′为另一常量），又因为ω△t=△θ（圆盘转过角度的变化量），因此有：对应任一小段时间△t，总有△θ∝△ω。

所以，从开始减速到停下的这段时间内，圆盘转过的角度正比于其角速度的改变量，即为：

θ1：θ2=ω0：2ω0=1：2。

（3）开关断开后，由于图1中磁场充满整个圆盘，使得圆盘沿每条半径方向的感应电动势都一样大，电荷只在盘心和盘边缘处积累，不会在圆盘内部形成电流（涡流），因此在开关断开后，只要没有其它的阻力，圆盘将匀速转动不会减速。图2中由于磁场存在于圆盘中的一部分区域内，使得开关断开后，仍有电流在圆盘内部形成回路（涡流），进而引起安培力使圆盘减速。因此这样的想法错误。