题目内容
【题目】一个阻值为R、匝数为n的圆形金属线圈与阻值为2R的电阻R1，电容为C的电容器连接成如图（a）所示回路。金属线圈的半径为r1， 在线圈中半径为r2的圆形区域内存在垂直于线圈平面向里的匀强磁场，磁感应强度B随时间t变化的关系图线如图（b）所示。图线与横、纵轴的截距分别为t0和B0.导线的电阻不计。求0至t1时间内：
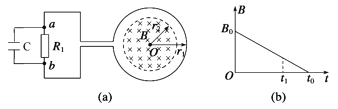
(1)通过电阻R1的电流大小和方向；
(2)通过电阻R1的电荷量q；
(3)t1时刻电容器所带电荷量Q。
【答案】(1) 
, 方向从b到a. (2) 
(3) 
【解析】
（1）由B-t图象的斜率读出磁感应强度的变化率
，由法拉第电磁感应定律求出线圈中产生的感应电动势，由欧姆定律求出感应电流的大小，由楞次定律判断出感应电流的方向；
（2）由公式q=It求出通过电阻R1上的电量q；
（3）再依据Q=CU，及U=IR1，即可求解。
（1）由B-t图象可知，磁感应强度的变化率为：
根据法拉第电磁感应定律，感应电动势：
根据闭合电路的欧姆定律，感应电流为：I1=
联立以上三式，解得：
根据楞次定律可知通过R1上的电流方向：从b到a
（2）通过R1的电荷量q=I1t1得：
（3）依据欧姆定律，则电容器两极电压为：U=I1R1=
；
再由电容器的电量为：Q=CU=
练习册系列答案
相关题目
