题目内容
【题目】如图所示，将质量为10 kg的小球用轻绳挂在倾角α＝45°的光滑斜面上，下列情况中斜面向右加速运动，小球相对斜面静止，问：(g取10 m/s2)
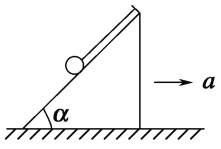
(1)当加速度a＝10／3 m/s2时，绳对小球的拉力多大 ？
(2)当绳对小球的拉力FT＝200 N时，它们的加速度多大？
【答案】（1）
（2）
【解析】
当加速度a较小时，小球与斜面一起运动，此时小球受重力、绳子拉力和斜面的支持力，绳子平行于斜面；当加速度a足够大时，小球将飞离斜面，此时小球仅受重力与绳子的拉力作用，绳子与水平方向的夹角未知，而题目要求出当斜面以10/3m/s2的加速度向右做加速运动时，绳的拉力及斜面对小球的弹力，必须先求出小球离开斜面的临界加速度a0，（此时小球所受斜面的支持力恰好为零）小球的受力如图：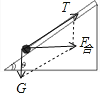
当小球对斜面的压力为零时，小球只受重力和拉力，合力水平向右
mgcot45°=ma
a=gcot45°=g=10m/s2
拉力T=mgtan45°=100N
（1）当斜面以加速度a=10/3m/s2沿图示方向运动时，小于10m/s2，所以斜面对球有弹力，
所以有：Fsin45°+Tsin45°=mg…①
Fcos45°-Tcos45°=ma…②
联立①②解得：
（2）当FT=200N＞100N时，小球将飞离斜面，此时小球受两个力作用；绳与水平方向的夹角为θ，则小球只受重力和绳拉力，两力的合力在水平方向，根据牛顿第二定律有：
竖直方向有：FTsinθ=mg
水平方向有：FTcosθ=ma
联列解得：a=10
m/s2
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
