题目内容
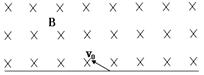
如图甲所示,两平行金属板A、B的板长L=0.2m,板间距d=0.2m,两金属板间加如图乙所示的交变电压,并在两板间形成交变的匀强电场,忽略其边缘效应。在金属板右侧有一方向垂直于纸面向里的匀强磁场,其左右宽度D=0.4m,上下范围足够大,边界MN和PQ均与金属板垂直,匀强磁场的磁感应强度B=1×10-2 T.现从t=0开始,从两极板左侧的中点O处以每秒钟1000个的数量均匀连续地释放出某种正电荷粒子,这些粒子均以v0=2×105 m/s的速度沿两板间的中线OO′连续进入电场,已知带电粒子的比荷=1×108C/kg,粒子的重力和粒子间的相互作用都忽略不计,在粒子通过电场区域的极短时间内极板间的电压可以看作不变.求:
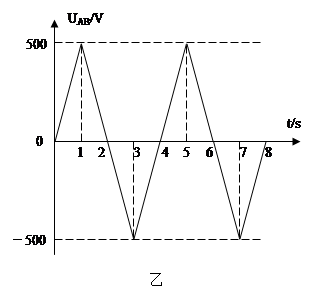
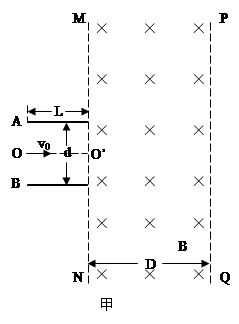
(1)t=0时刻进入的粒子,经边界MN射入磁场和射出磁场时两点间的距离;
(2)在0~1s内有多少个带电粒子能进入磁场;
(3)何时由O点进入的带电粒子在磁场中运动的时间最长?
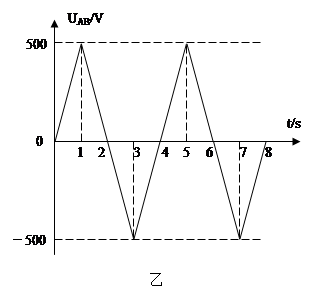
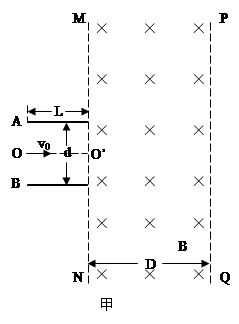
(1)t=0时刻进入的粒子,经边界MN射入磁场和射出磁场时两点间的距离;
(2)在0~1s内有多少个带电粒子能进入磁场;
(3)何时由O点进入的带电粒子在磁场中运动的时间最长?
(1)0.4m(2)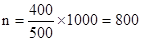 (3)t=4n+0.6(s)或t=4n+1.4(s) (n=0,1,2……)
(3)t=4n+0.6(s)或t=4n+1.4(s) (n=0,1,2……)
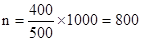 (3)t=4n+0.6(s)或t=4n+1.4(s) (n=0,1,2……)
(3)t=4n+0.6(s)或t=4n+1.4(s) (n=0,1,2……)(18分,每问6分)
解:(1)t=0时刻,电压为0,粒子匀速通过两板进入磁场,
 (2分)
(2分)
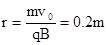 (2分)
(2分)
r<D,则粒子在MN边界射出磁场。
入射点和出射点的距离为s=2r=0.4m (2分)
(2)粒子在两板间做类平抛运动,刚好打到板最右端时,
L=v0t1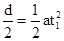
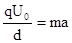 (3分)
(3分)
U0=400V (1分)
则0~1s内能够进入磁场的粒子个数为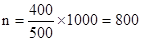 (2分)
(2分)
(3)假设两板加电压为U时,粒子向下偏转并进入磁场,刚好与磁场PQ边界相切,
在磁场中,
由几何关系得,R+Rsinθ=D (2分)
在电场中,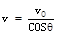
联立解得:θ=370

U=300V (2分)
U<U0=400V,则当两板电压U=300V,且粒子向下偏转时,粒子在磁场中运动的时间最长,对应入射的时刻为
t=4n+0.6(s)或t=4n+1.4(s) (n=0,1,2……) (2分)
本题考查的是带电粒子在电场和磁场中运动的情况,由于t=0时刻粒子匀速直线通过电场,垂直边界进入磁场,在磁场中作匀速圆周运动,做半周运动射出磁场,只需计算出圆周运动的半径,即可;粒子在两板间做类平抛运动,刚好打到板最右端时,能进入磁场,根据这个条件算出能进入磁场的粒子个数;根据洛伦兹力的方向可知向下偏转时粒子进入磁场的运动时间最长,根据几何关系可以得到粒子运动时间最长时两板的电压,从而的到粒子入射时刻。
解:(1)t=0时刻,电压为0,粒子匀速通过两板进入磁场,
 (2分)
(2分)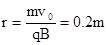 (2分)
(2分)r<D,则粒子在MN边界射出磁场。
入射点和出射点的距离为s=2r=0.4m (2分)
(2)粒子在两板间做类平抛运动,刚好打到板最右端时,
L=v0t1
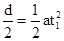
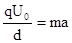 (3分)
(3分)U0=400V (1分)
则0~1s内能够进入磁场的粒子个数为
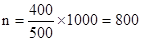 (2分)
(2分)(3)假设两板加电压为U时,粒子向下偏转并进入磁场,刚好与磁场PQ边界相切,
在磁场中,

由几何关系得,R+Rsinθ=D (2分)
在电场中,
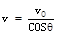
联立解得:θ=370

U=300V (2分)
U<U0=400V,则当两板电压U=300V,且粒子向下偏转时,粒子在磁场中运动的时间最长,对应入射的时刻为
t=4n+0.6(s)或t=4n+1.4(s) (n=0,1,2……) (2分)
本题考查的是带电粒子在电场和磁场中运动的情况,由于t=0时刻粒子匀速直线通过电场,垂直边界进入磁场,在磁场中作匀速圆周运动,做半周运动射出磁场,只需计算出圆周运动的半径,即可;粒子在两板间做类平抛运动,刚好打到板最右端时,能进入磁场,根据这个条件算出能进入磁场的粒子个数;根据洛伦兹力的方向可知向下偏转时粒子进入磁场的运动时间最长,根据几何关系可以得到粒子运动时间最长时两板的电压,从而的到粒子入射时刻。

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
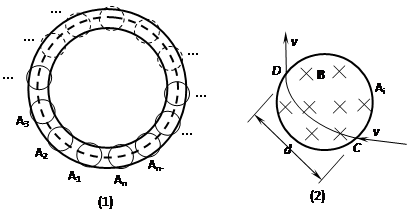
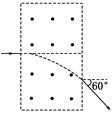

 的均匀磁场,其方向垂直于纸面向里.在圆形区域平面内固定放置一绝缘材料制成的边长为L=1.2a的刚性等边三角形框架
的均匀磁场,其方向垂直于纸面向里.在圆形区域平面内固定放置一绝缘材料制成的边长为L=1.2a的刚性等边三角形框架 ,其中心
,其中心 位于圆形区域的圆心.
位于圆形区域的圆心. 边上
边上 点(DS=L/2)处有一发射带电粒子源,发射粒子的方向皆在图示平面内且垂直于
点(DS=L/2)处有一发射带电粒子源,发射粒子的方向皆在图示平面内且垂直于 (>0),质量皆为
(>0),质量皆为 ,但速度
,但速度 有各种不同的数值.若这些粒子与三角形框架的碰撞均无机械能损失,并要求每一次碰撞时速度方向垂直于被碰的边.试问:(1)若发射的粒子速度垂直于
有各种不同的数值.若这些粒子与三角形框架的碰撞均无机械能损失,并要求每一次碰撞时速度方向垂直于被碰的边.试问:(1)若发射的粒子速度垂直于