题目内容
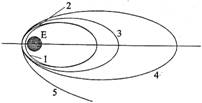（21分）嫦娥1号奔月卫星与长征3号火箭分离后，进入绕地运行的椭圆轨道，近地点离地面高
，远地点离地面高
，周期约为16小时，称为16小时轨道（如图中曲线1所示）。随后，为了使卫星离地越来越远，星载发动机先在远地点点火，使卫星进入新轨道（如图中曲线2所示），以抬高近地点。后来又连续三次在抬高以后的近地点点火，使卫星加速和变轨，抬高远地点，相继进入24小时轨道、48小时轨道和地月转移轨道（分别如图中曲线3、4、5所示）。已知卫星质量
，地球半径
，地面重力加速度
，月球半径
。
1．试计算16小时轨道的半长轴a和半短轴b的长度，以及椭圆偏心率
。
2．在16小时轨道的远地点点火时，假设卫星所受推力的方向与卫星速度方向相同，而且点火时间很短，可以认为椭圆轨道长轴方向不变。设推力大小
，要把近地点抬高到600
，问点火时间应持续多长？
3．试根据题给数据计算卫星在16小时轨道的实际运行周期。
4．卫星最后进入绕月圆形轨道，距月面高度
约为200，周期
分钟，试据此估算月球质量与地球质量之比值。
解析：
1. 椭圆半长轴a等于近地点和远地点之间距离的一半，亦即近地点与远地点矢径长度（皆指卫星到地心的距离）
与
的算术平均值，即有
(1)
代入数据得
km (2)
椭圆半短轴b等于近地点与远地点矢径长度的几何平均值，即有
(3)
代入数据得
(4)
椭圆的偏心率
(5)
代入数据即得
(6)
2. 当卫星在16小时轨道上运行时，以
和
分别表示它在近地点和远地点的速度，根据能量守恒，卫星在近地点和远地点能量相等，有
(7)
式中
是地球质量，
是万有引力常量. 因卫星在近地点和远地点的速度都与卫星到地心的连线垂直，根据角动量守恒，有
(8)
注意到
(9)
由(7)、(8)、(9)式可得
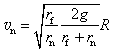(10)
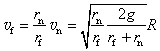(11)
当卫星沿16小时轨道运行时，根据题给的数据有
由(11)式并代入有关数据得
km/s (12)
依题意，在远地点星载发动机点火，对卫星作短时间加速，加速度的方向与卫星速度方向相同，加速后长轴方向没有改变，故加速结束时，卫星的速度与新轨道的长轴垂直，卫星所在处将是新轨道的远地点.所以新轨道远地点高度
km，但新轨道近地点高度
km.由(11)式，可求得卫星在新轨道远地点处的速度为
km/s (13)
卫星动量的增加量等于卫星所受推力F的冲量，设发动机点火时间为t，有
(14)
由(12)、(13)、(14)式并代入有关数据得
t=
(约2.5分) (15)
这比运行周期小得多.
3. 当卫星沿椭圆轨道运行时，以r表示它所在处矢径的大小，v表示其速度的大小，
表示矢径与速度的夹角，则卫星的角动量的大小
(16 )
其中
（17）
是卫星矢径在单位时间内扫过的面积，即卫星的面积速度.由于角动量是守恒的，故
是恒量.利用远地点处的角动量，得
(18)
又因为卫星运行一周扫过的椭圆的面积为
(19)
所以卫星沿轨道运动的周期
(20)
由(18)、(19)、(20) 式得
(21)
代入有关数据得
s (约15小时46分) (22)
注：本小题有多种解法.例如，由开普勒第三定律，绕地球运行的两卫星的周期T与T0之比的平方等于它们的轨道半长轴a与a0之比的立方，即
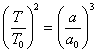
若
是卫星绕地球沿圆轨道运动的轨道半径，则有
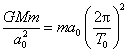
得 
从而得
代入有关数据便可求得(22)式.
4. 在绕月圆形轨道上，根据万有引力定律和牛顿定律有
(23)
这里
是卫星绕月轨道半径，
是月球质量. 由(23)式和(9)式，可得
(24)
代入有关数据得
(25)
我国整个探月工程分为“绕”、“落”、“回”3个阶段．第一期绕月工程已于2007年10月24日发射探月卫星“嫦娥一号”，这是我国航空航天领域的又一壮举，“嫦娥一号”将对月球表面环境、地貌、地形、地质构造与物理场进行探测．设想2016年一名中国宇航员乘“嫦娥奔月号”飞船登上月球，并在月球表面用单摆做实验．