题目内容
我国整个探月工程分为“绕”、“落”、“回”3个阶段．第一期绕月工程已于2007年10月24日发射探月卫星“嫦娥一号”，这是我国航空航天领域的又一壮举，“嫦娥一号”将对月球表面环境、地貌、地形、地质构造与物理场进行探测．设想2016年一名中国宇航员乘“嫦娥奔月号”飞船登上月球，并在月球表面用单摆做实验．（1）在“用单摆测定重力加速度”的实验中：测摆长时，若正确测出悬线长为l和摆球直径为d，则摆长为
l+
| d |
| 2 |
l+
；| d |
| 2 |
测周期时，当摆球经过
平衡位置
平衡位置
位置时，计时并计数1次，测出经过该位置N次（约60--100次）的时间为t，则周期为| 2t |
| N-1 |
| 2t |
| N-1 |
（2）根据月球表面的单摆实验，描绘出了单摆周期的平方与摆长的关系，即T2-L的图象，如图所示，已知月球的半径R为1.6×106m，
则：月球表面的重力加速度为
1.6m/s2
1.6m/s2
；“嫦娥奔月号”飞船绕月飞行的最小周期为2000πs
2000πs
．分析：（1）单摆摆长等于摆线的长度与摆球半径之和，先测出半球直径，然后组装好单摆，然后测出摆线的长度，两者之和是摆长．
一次全振动经过平衡位置两次．
（2）由题意公式g=
得到T2=
，图象斜率表示
，结合图象数据得到重力加速度．
根据万有引力提供向心力求出最小周期
一次全振动经过平衡位置两次．
（2）由题意公式g=
| 4π2l |
| T2 |
| 4π2l |
| g |
| 4π2 |
| g |
根据万有引力提供向心力求出最小周期
解答：解：（1）若正确测出悬线长为l和摆球直径为d，则摆长为l+
测周期时，当摆球经过平衡位置位置时，计时并计数1次，测出经过该位置N次（约60--100次）的时间为t，
周期T=
（2）由题意公式g=
得到T2=
，图象斜率表示
，
结合图象数据得到
g=1.6m/s2．
根据万有引力提供向心力得
“嫦娥奔月号”飞船绕月飞行的最小周期T=2π
根据黄金代换GM=gR2得
T=2000πs
故答案为：（1）l+
；
平衡位置；
（2）1.6m/s2；2000πs
| d |
| 2 |
测周期时，当摆球经过平衡位置位置时，计时并计数1次，测出经过该位置N次（约60--100次）的时间为t，
周期T=
| 2t |
| N-1 |
（2）由题意公式g=
| 4π2l |
| T2 |
| 4π2l |
| g |
| 4π2 |
| g |
结合图象数据得到
g=1.6m/s2．
根据万有引力提供向心力得
“嫦娥奔月号”飞船绕月飞行的最小周期T=2π
|
根据黄金代换GM=gR2得
T=2000πs
故答案为：（1）l+
| d |
| 2 |
平衡位置；
| 2t |
| N-1 |
（2）1.6m/s2；2000πs
点评：本题考查了应用单摆测重力加速度的实验原理，通过图象的函数表达式得到斜率的物理意义．
练习册系列答案
相关题目
2004年1月，我国月球探测工程经国务院正式批准立项后，该工程被命名为“嫦娥工程”，整个探月工程将分为三期完成，要突破“绕”、“落”和“回”三大关键技术．第一颗绕月卫星命名为“嫦娥一号”，并且“嫦娥二号”于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空，并获得了圆满成功．
据报道，2007年10月24日18时05分04.602秒我国的“嫦娥一号”卫星成功发射升空！圆了中国人几千年的梦想．我国整个探月工程分为“绕”、“落”、“回”3个阶段，第一期绕月工程就是通过发射探月卫星“嫦娥一号”，对月球表面环境、地貌、地形、地质构造与物理场进行探测．设嫦娥一号对月球进行科学探测时离月球表面的高度为h，周期为T，月球的半径为R，则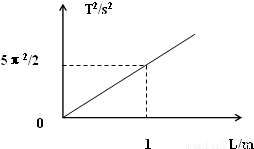
2004年1月，我国月球探测工程经国务院正式批准立项后，该工程被命名为“嫦娥工程”，整个探月工程将分为三期完成，要突破“绕”、“落”和“回”三大关键技术．第一颗绕月卫星命名为“嫦娥一号”，并且“嫦娥二号”于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空，并获得了圆满成功．
，式中各量分别为：返回舱与宇航员的总质量为m，月球表面的重力加速度为g，月球半径为R，轨道舱到月球中心的距离为r，如图乙所示．不计月球表面大气等对返回舱的阻力和月球自转的影响，则该宇航员乘坐的返回舱从月球表面要能返回轨道舱，至少需要获得动能Ek为多少？